算法课程概述。

问题

  1. 计算机能够解决的问题

    1. 数值计算问题

    2. 非数值计算问题

  2. NP问题、Non-NP问题、P问题、NP-H、NP完全问题

    图示（待补充）

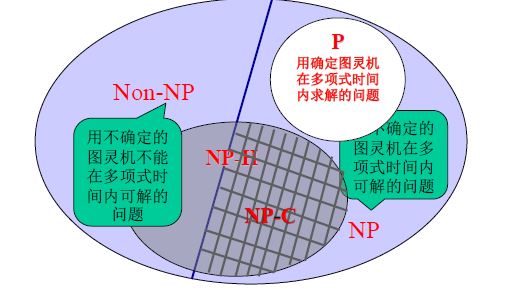
    计算问题分类

    1. 问题分为NP问题和Non-NP问题

      NP就是指非确定图灵机在多项式时间里可解的问题。

      Non-NP就是非确定图灵机在多项式时间内不可解。

      非确定图灵机 : 每一步的执行不是确定的。对立面是确定的图灵机，每步按照基础指令确定的执行。当前的计算机是确定的图灵机。

      多项式时间： 多项式，即 $ n $ , $ n^2 $ , $ nlog n $之类的。$x^n$是关于n的非多项式，是关于n的指数形式。

    2. P问题

      P问题是完全属于NP问题的子集。 P问题是指用确定图灵机可在多项式时间内可解的问题。

    3. NP-H及NP完全问题

      NP-H是指很难的NP问题？但是NP-H很跨NP和None-NP，而NP-H中属于NP的部分就被称为NP完全问题。

      目前面对NP完全问题，计算机只能拿到近似解。

算法设计与分析的一些定义

  1. 面向的问题

    1. P问题（求精确解）

      包含 分治算法 ， 动态规划算法， 贪心（精确解）算法 ， 搜索策略， 平摊算法

    2. NP完全问题（非精确解）

      包含近似算法(Approximate)，随机算法(Random)

    PS : 除了以上提及的算法，还会讲目前流行的On-line算法

  2. 时间史

    20世纪70年代之前没有算法

    直到Donald Ervin Knuth的The Art of Computer Programming , 提出了算法的概念并开创了计算机科学与技术这门学科。

    大牛们 ： Edsger W.Dijkstra , Stephen Arthur Cook , Richard M.karp , 姚期智

  3. 解决一个问题的过程

    可计算否(计算理论) -> 能行可计算否（计算复杂性理论） -> 设计与分析算法（算法设计与分析） -> 用计算机实现算法（数据结构与程序设计） -> 软件流（编译与OS）

  4. 计算 ， 算法

    可由一个给定计算模型机械地执行规则或计算步骤序列称为该计算模型的一个计算。

    • 程序是一个计算

    • 不能终止的算法不是计算

    算法： 算法是满足以下条件的计算

    1. 终止性

    2. 确定性

      每步都是严格定义和确定的动作

    3. 能行性

      每个动作都能够被精确地机械执行

    4. 明确的输入、输出

    最早的算法是欧几里得的最大公因子问题

    输入 -> F -> 输出

    F就是定义从输入到输出的处理序列

  5. 分析算法

    • 正确性分析

      每个输入都停止；每个输入都有正确的输出（对近似算法，要求较大概率产生近似正确的解且产生不多的不正确的解）；

      正确性分析是必要的。

      不能认为某些实例上的正确就推出算法的正确 -> 不能说实现的程序正确就反过来说明算法的正确。

    • 复杂性分析

      分析算法对不同输入的资源需求

      哪些资源？ 时间、空间、IO

      复杂性是输入大小的函数

      定义输入大小，具体实例的时间复杂性、具体实例的空间复杂性、算法的最坏复杂性就是所有实例中最坏的那个，算法的最小复杂性是所有实例中最小复杂性；算法的平均复杂性是求所有实例复杂性的期望（$\bar{Complexity} = \sum_{x \in input}{p_x \cdot Complexity(x)}$）

参考资料

  1. Introduction to Algorithm (算法导论)

  2. Approximation Algorithm

  3. Randomized Algorithm

Journals : Algorithmica

Conference