算法设计与分析-课后总结3

从第三节课后半段到第四节课，主要讲了分治算法。分治算法包含分,治,合三个过程。其中“分”与“合”一般是分治能够优化时间效率的关键。“治”一般是以分割的子问题作为输入递归调用算法。包含的例子有：“n位二进制整数乘法”，“矩阵乘法”，“找最近点对。”

分治算法概述

分治算法一般包含3个步骤：

分 (Divide)

将大问题（按照某种条件）拆分为小问题。[算法关键]

记时间复杂度为 $ T_{divide}(n) = D(n)$
治 (Conquer)

以子问题作为输入，递归调用算法，直到遇到边界条件。

设分为$a$个子问题，每个子问题的规模为原规模的$\frac{1}{b}$ ，记时间复杂度为$T_{conquer}(n) = aT(\frac{n}{b})$
合 (Combine / Merge)

对每个子问题合并结果。[算法关键]

记时间复杂度为 $T_{merge}(n) = C(n)$

总时间复杂度为$T(n) = aT(\frac{n}{b}) + D(n) + C(n)$

分治的例子

在排序中的应用
1. 归并排序 MERGE-SORT
  1. 将待排序数组按照位置（前一半、后一半）分为两个部分。
  2. 递归调用，直到数组大小为1（认为单个数的数组是有序的）；
  3. 合并。此时左右两部分的数组都是有序的，只需比较两部分的头部元素，线性时间内即可完成归并完成。
  代码见Merge Sort
  
  该代码仿写自维基百科-归并排序
2. 快速排序 QUICK-SORT
  1. 选择一个基准元素（pivot），大于它的组成一个数组，小于等于它的又组成一个数组。
    
    基准元素通常选最后一个，或者第一个。选择过程中需要忽略该元素。
    
    归并时加上即可；或者也可以加入到某个子数组中。
  2. 递归调用，当子数组只有一个时，递归调用过程结束，开始返回。
  3. 合并非常简单，合并即可。直接左右合并在一起即可。(实际中不对应任何代码，因为是原地排序，合并已经在子数组排序后已经完成。)
    
    如果基准元素未放入子数组中，则合并时将其放入中间。
    
    代码见Quick-Sort
    
    仿写自维基百科-快速排序
都使用了分治的思想，但是分的过程不同；Merge Sort分非常简单，没有考虑大小关系，所以合并的时候需要比较大小；快排分的时候就保证了左右两边的相对整体的有序，所以合并时就非常简单。可以认为这是在优化分和合的不同步骤。
整数乘法

优化分的例子

问题描述：

输入 : 2个均为n位的二进制数X与Y

输出 : X与Y的乘积

乘法的本质是转换到加法来做。

两个n位二进制数相乘，直接做，需要做可以认为需要做两个$1 \to n$的循环，复杂度为$O(n^2)$

使用分治方法，我们可以把n位的二进制数分为两半，分别运算，再合并。

直观的分治策略：

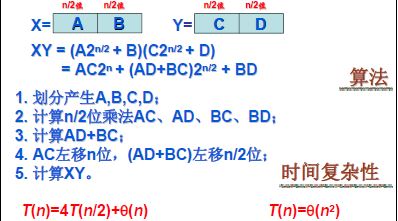
我们发现算法的复杂度并没有得到优化。我们可以尝试优化分的过程。

优化的分治策略：

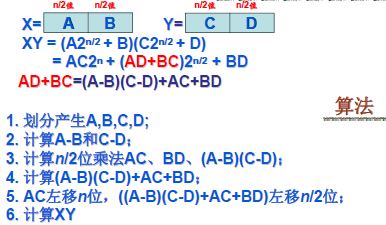
比较神奇的方式~ 减少了乘法的数量，我们的复杂度递归方程变为：

$T(n) = 3T(\frac{n}{2}) + O(n)$

使用Master定理，得到复杂度为$T(n) = O(n^(lg3)) = O(n^{1.59})$
矩阵乘法

类似上述整数乘法。

输入 : 两个$n \times n$的矩阵A , B 。

输出 : 矩阵乘法结果。

矩阵乘法的过程：
```
 for i <- 1 , n 
     for j <- 1 , n
         $a_{ij} = \sum_{k=1}^{k=n}A_{ik}B_{kj}$ 
```
易知其复杂度为$O(n^3)$

分治法我们把每个矩阵都分为等大的四个矩阵。

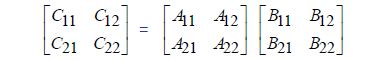
根据矩阵乘法，有
\[C_{11} = A_{11} \times B_{11} + A_{12} \times B_{21}\] \[C_{12} = A_{11} \times B_{12} + A_{12} \times B_{22}\] \[C_{21} = A_{21} \times B_{11} + A_{22} \times B_{21}\] \[C_{22} = A_{21} \times B_{12} + A_{22} \times B_{22}\]
如果分治法直接按照上述方法做分割，那么递归方程为 $T(n) = 8T(n/2) + O(n^2)$ , 由Master定理，其复杂度为$T(n) = \Theta(o^3)$

所以我们需要如上面的整数乘法一般，进行一些变换，来达到减少乘法运算（子问题）的目的。

变换结果如下（真的不知道怎么弄出来的 = =）：

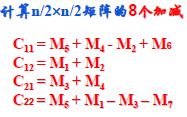
如此得到的结果：
找最近点对

优化合的过程。

输入： Euclidean空间上的n个点的集合Q

输出： $P_1 , $P_2 \in Q$ , $Dis(P_1 , P_2) = Min{Dis(X , Y) X , Y \in Q}$

一维空间的情况
1. 基于排序的方法
  
  一维空间下，点可以经过排序变为在坐标轴上顺序的点。故最近的点必然是相邻的点。所以只需考察相邻点的距离即可。
  
  排序时间$O(n\lg n)$ , 找最近时间为$O(n)$（每个点都需要算一次） ,故算法总时间开销是$O(n\lg n)$
2. 基于分治的方法
  1. 线性时间内找到所有点的中位点（x = m），然后将其划分为左边点集合和右边点集合
  2. 递归划分，直到只有两个点或一个点：两个点时，最近点对就是这两个点；一个点时，返回空；
  3. 开始合并，合并后的最近点对，有三种情况——
    1. 左边的最近点对
    2. 右边的最近点对
    3. 跨越中位线，即左边最右的点与右边最左的点构成的点对。
    如上即能完成合并。~~认为合并时$O(1)$的~~。合并是$O(n)$的，因为没有排序，所以找左边最右与右边最左是一个$O(n)$的消耗。
  $T(n) = 2T(\frac{n}{2}) + O(n)$ ，根据Master定理,满足第二种情况，有$T(n) = O(n \lg n)$
二维空间的情况

采用分治的方法。

首先进行排序——按照x坐标、y坐标递增排序。
1. 划分。找到中位线$x=m$尽量将点集分为相等的两部分。
2. 当点集只有两个点或者一个点时，递归划分结束；如果有两个点，则返回该点对；否者返回空；
3. 合并。同样最近点对只可能有三种情况。只是第三种情况较一维时复杂了很多。
  
  三种情况分别为：
  1. 左边点集的最近点对，记最近距离为$d_l$
  2. 右边点集的最近点对，记最近距离为$d_r$
  3. 跨越中位线的点对
  第三种情况，由于在二维空间中，我们不能直观的认为像一维那般，在左边找横坐标最大，在右边找横坐标最小的点，作为跨越中位线点对的最近点对——因为还有纵坐标的影响。但是我们肯定不能极端地比较所有点的距离，不然这里是$O(n)$，那么递归方程$T(n) = 2 T(\frac{n}{2}) +O(n^2)$ , 得到的时间复杂度就是$O(n^2)$，相较与暴力枚举，没有太大的优势；所以我们必须要优化合的过程。
  
  比较直观的优化是，由于我们已经得到了最左点集合最右点集中点对的最小距离，那么跨越中位线的点对距离必须必其中的最小距离小，才能成为合并后的最小距离的点对.我们记两边集合中最小的点对距离为$d$,即$d = min(d_l , d_r)$所以我们可以相较宽松的在中位线附近确定一个$x= m \pm d$的邻域。只有这个邻域内的点对才有可能有最小距离。同时，由于距离的对称性，我们可以只以左边的点为基准，去找每个左边邻域的点与右邻域的点的距离。
  
  更进一步的确定搜索空间，当然也比较宽松，对左边邻域的一个点$m(x,y)$，其真正有效的搜索邻域是以$(m,y+d)$为左上角，$(m+d,y-d)$为右下角的矩形。这个搜索区域已经扩展了很多次——首先忽略了左边的领域内的区域、其次本来是圆形的搜索空间，这里直接用矩形代替。这样虽然扩大了搜索空间，不过实际上也减少了计算量。算是一个不错的权衡。
  
  而且，我们可以证明，在上面确定的长为$2d$、宽为$d$的矩形中，最多存在6个点。
  
  证明：我们把该矩形分为长为$\frac{2d}{3}$，宽为$\frac{d}{2}$的6个小矩形，如果有7个点点放入其中，由鸽洞原理，则某个小矩形中至少有2个点。而每个小矩形的最大距离（对角线距离）为$\frac{5d}{6}$，即小于d。而我们的$d$是左右集合中最小点对距离，所以这种情况是不可能的。所以最多6个点！
  
  这样，我们证明了在此邻域内搜索，时间时线性的，且小于$6n$，即$O(n)$
由此递归方程为$T(n) = 2T(\frac{n}{2}) + O(n)$，时间复杂度为$O(n\lg n)$
分治地寻找凸包问题

这里目前还没有看懂。需要写完代码后才能明白。