主要讲前馈神经网络中的相关知识,包括线性分类器的局限性、神经网络的表达能力、结构介绍、BP算法、加冲量。
编辑中
线性分类的局限性
对于线性可分的样本集,我们使用线性分类器就能得到满意的结果。但面对线性不可分的样本集,基于线性的分类就不能适应了。我们就说线性分类器的表达能力仅能处理线性可分的数据集。
例如,对于异或问题,线性分类器就不能够解决。
在前面的课程中讲过,如果我们能够扩展样本表达所在的空间维度,即升维,那么原本线性不可分的样本,在高维空间中也许就能够线性可分了。我们定义一个函数F,其输入是当前空间维度下的样本表示,输出是高维空间下的样本表示。一个实例:
\[F( (x_1 , x_2) ) = (x_1 , x_2 , \alpha x_1 x_2 )\]书上的一个例子,经过该空间变换,就可以在高维空间中找到一个线性函数来分开样本了。
以上就是线性分类器的局限性以及在该局限性下人们可能采取的方法——核函数。这也是SVM的一个特征。
在*A Course in Machine Learning *中似乎提到过,对于线性不可分的问题,一种方法是使用核函数映射到高维空间,另一种当然就是使用非线性的分类方法。神经网络就属于非线性的分类方法。
神经网络的定义及其表达能力
(人工)神经网络(Artificial Neural Networks)这个称呼的由来,就说明了这是人们大脑仿生的一种尝试。
PPT上定义说,神经网络是多层感知器的组合。以前也这么理解,不过上次看了Neural Networks and Deep Learning里sigmoid 神经元一章,也接受了感知器与sigmoid神经元不是一个东西这么一个概念。虽说很多东西都是很像的,它们产生时往往都是很相关的,不过我们后来去定义它们的时候,为了规范化以及消歧,往往就限定了其含义。我们这里也理解为:
神经网络是多层sigmoid神经元的组合。每层之间的节点是全连接的。
sigmoid神经元对输入做了非线性变换,且多层次连接,最终得到一个非线性的分类界面。其表达能力很强(高适应性 , high flexibility)。
以下贴两个PPT上的图来形象地说明神经网络是如何拥有高适应的表达能力的:
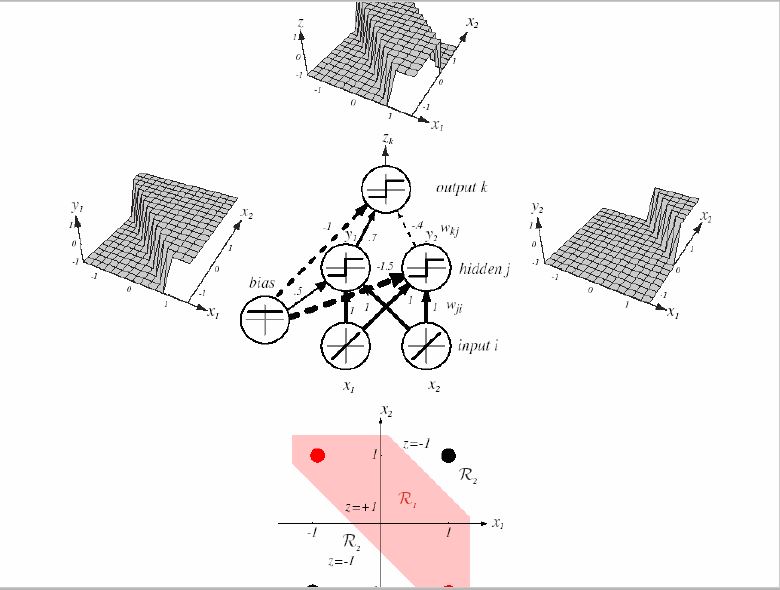
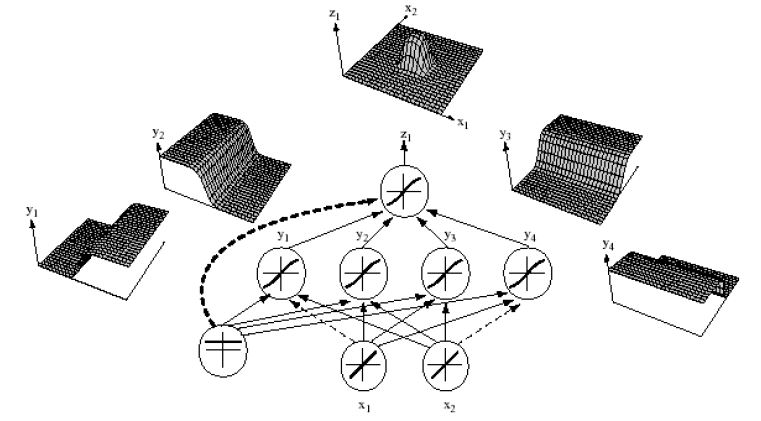
第一个图用一个简单的3层神经网络完成了异或的表达;
第二图则形象地展示了如何从一个个简单的分类面通过非线性组合形成最终的复杂非线性分类界面。
我们注意到单纯的一个sigmoid神经元,在空间产生的是一个sigmoid形状(即S型)的分类面。通过下一层(隐层或输出层,图中是输出层)的非线性变换(线性组合,加以非线性激活函数),变为了一个非线性分类界面。
神经网络结构介绍
包含 输入层 , 隐层, 输出层。昨天看word2vec的一个介绍,看到说可以看做4层,其中输入层到隐层间加一个投影层,这个应该不是关键。
一般书上给的结构都比较简单,就是几个圆圈连上,但是在推BP求导的时候,竟然发现自己对于网络的结构还是认识不清的。突然想到,如果我们要真正的写代码,那么一个sigmoid节点类该如何定义呢?
class Sigmoid
{
node output ;
node input[N] ;
double weights[N] ;
double net ;
processing sigmoid ;
processing sigma ;
}
每个节点,都有$N$个输入,$N$个权值向量(如果有偏移存在,则表示增广向量),然后对应一个$\sum$操作,得到净输入值(net)。这是对输入线性组合的结果。对净输入值,有$\sigma(net) = \frac{1}{1 + e^{-net}}$操作,得到一个非线性变换后的输出。
把这些节点一层一层按照上述结构组合起来,才构成了一个神经网络。一定要画出来。如下图:
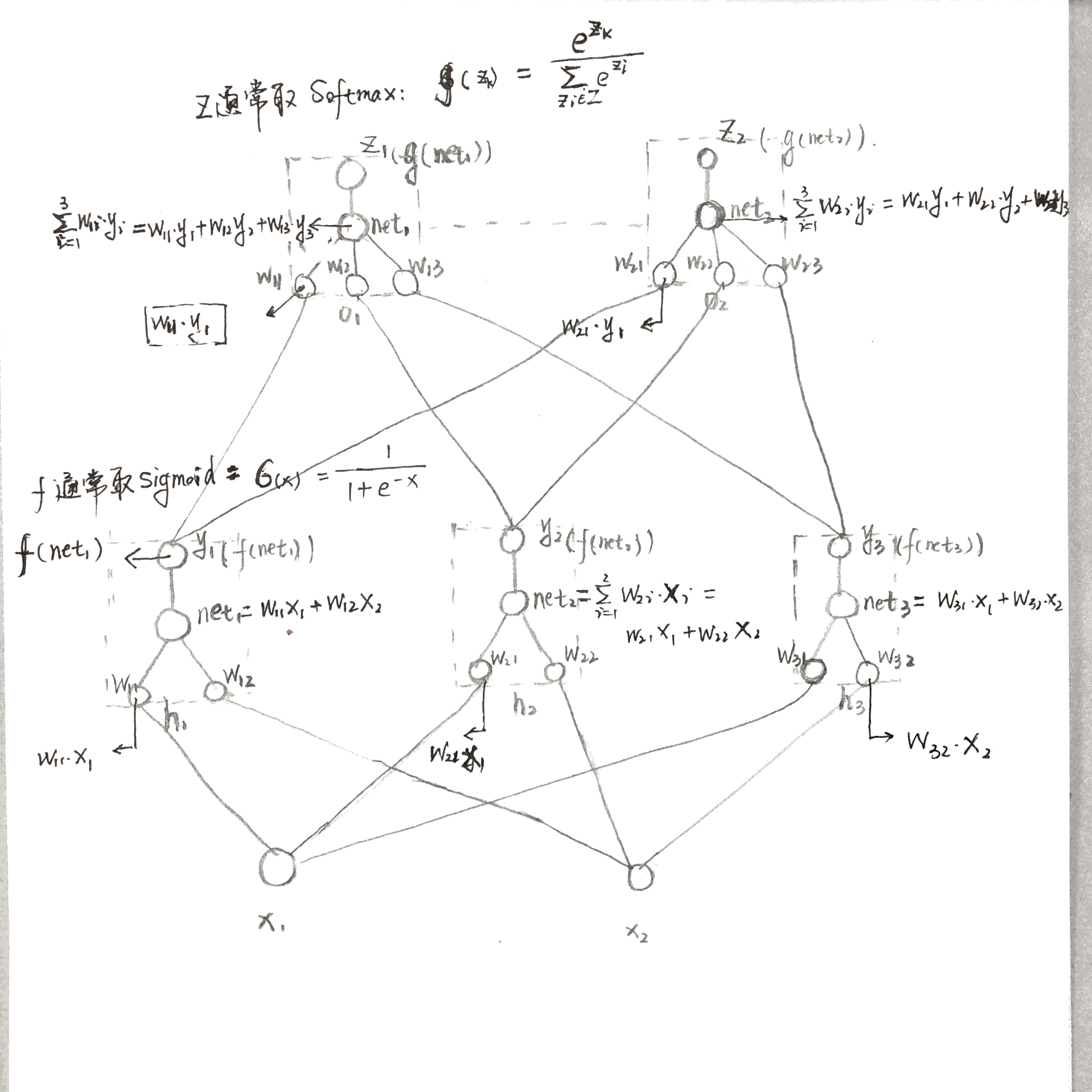
注意到在模式识别中提出来的概念:净输入值。
\[net = W ^T X = \sum_{i=1}^d w_i x_i\]就是个输入变量与对应权值的线性组合部分。在其他地方都没有一个明确的称呼,在模式识别中将其称为“净输入值”,还是非常不错的~至少有名字啦~到这里还是线性的。
接着就是激活函数$f$了,在模式识别中也称为转移函数(transfer function)。激活函数常用的选择就是sigmoid函数(常记为$\sigma$):
\[\sigma(net) = \frac{1}{ 1 + e^{-net}}\]它的定义域是$(- \infty , + \infty)$ , 值域是$(0 , 1)$ , 过点$(0,0.5)$ ,单调递增的。这可以认为是signum函数(或者称为step function)的平滑版本(当然,其值域是有区别的,这么来说,signum函数与tanh函数更像)。
$\sigma(x)$的导数是:$\sigma(x)(1 - \sigma(x))$
注意,sigmoid函数也叫logstic函数。所以,这个也是逻辑回归啦。
确切的讲,逻辑回归,是指假设样本集满足逻辑斯谛分布,那么实例属于正例的条件概率就是这个逻辑斯谛函数的表示形式。
上述表示还是不太准确,仅作为一个联想吧
今天(已经是下一节课了)老师讲了,如果神经网络中没有这个非线性变换的函数,那么不管这个网络有多少层,它始终不能得到非线性的分类面(这个之前在本子上推过,不过加多少层,变的都是变量前的系数,所以永远都是线性的)。不过,这种多层的线性是有可能解决异或问题的?(当时老师似乎是这么说的,但是一细想,觉得也不太对!既然不管怎么组合都是线性的,那就还是一个线性分类面,肯定还是不能分类的)
BP算法
真正关键的地方啦。
我们首先要定义损失函数(目标函数):
\[J(W) = \frac{1}{2}\sum_{i=1}^k(T_i - Z_i )^2\]这个应该是用MSE均方误差来作为误差函数的(然而不除以K真的算均方误差吗?当然其实这个对于模型的训练无所谓了,前面的$\frac{1}2{}$也仅仅是为了求导方便)。
损失函数中,$k$表示输出节点的个数;$T_i$表示第$i$个输出节点的期望输出值(如果该实例是该类别,那就期望是1,否则就期望是0);$Z_i$表示该输出节点实际输出值。
\[\begin{align*} Z_i &= f(net_i) \\ net_i &= W_i ^T Y = \sum_{j=1}^m w_{ij} y_j \end{align*}\]为什么写作$J(W)$啊,明明里面根本就没有W啊~ 注意到我们的$Z$是与W相关的啊。
其中的$W_i$表示第$i$个输出节点的权值,权值的数量$m$表示隐层节点的个数,$w_{ij}$表示第$i$个输出节点的权值向量中对于第$j$个隐层输出想对应的权值。$y_j$当然表示第$j$个隐层的输出啦,这里用$y$表示或许有些歧义,不过这里就用来表示隐层的输出值了。
我们要求$J(W)$对于第$i$个输出节点中与第j个隐层输出相连的权值$W_{ij}$的导数,可以形式化的写作:
\[\begin{split} \frac{\partial J(W)}{\partial w_ij} &= \frac{\partial J(W)}{\partial Z_i} \frac{\partial Z_i }{\partial net_i } \frac{\partial net_i }{ \partial w_{ij} } \\ &=(Z_i - T_i) f'(net_i) y_j \end{split}\]这个是没有问题的~ 求导的链式法则嘛~ 那BP有意思在哪里呢?
我们注意到,损失值对于该输出节点的每个权值$W_{ij}$,其中$\frac{\partial J(W)}{\partial Z_i} \frac{\partial Z_i }{\partial net_i }$($(Z_i - T_i) f’(net_i) $)都是一样的,我们将其记为
\[\begin{equation} \label{oSensitivity} \delta_i = (Z_i - T_i) f'(net_i) \end{equation}\]$\delta_i$也被称为输出节点$i$的敏感度(sensitivity , 不知道是不是这么翻译)。这个值对每个特定的输出节点都是相同的,对于该节点的与第$j$的隐层输出相对应的权值向量的导数,可以表示为
\[\begin{equation} \label{ogradient} \frac{\partial J(W)}{\partial w_{ij}} = \delta_i y_j \end{equation}\]这么一来,就简化了形式,减少了计算量!而且给人的感觉非常神奇~
以上,由$(\ref{oSensitivity})(\ref{ogradient})$,每个输出节点$O_i$中的每个权值$W_ij$都能够算出来了。
接着我们算隐层节点j中与输入k(或者,如果下一层依然是隐层,那么就是下一隐层的节点k)相对应的权值$w_{jk}$在对于损失函数$J(W)$的梯度。
\[\begin{split} \frac{\partial J(W)}{\partial w_{jk}} &= \sum_{i=1}^{c} \big ( ~ \frac{\partial J(W)}{\partial Z_i} \frac{\partial Z_i }{\partial net_i } \frac{\partial net_i }{ \partial y_{j} } ~ \big ) \frac{\partial y_j }{\partial net_j } \frac{\partial net_j}{ \partial w_{jk}} \\ &=\sum_{i=1}^c \big ( ~ \delta_i w_{ij} ~ \big ) f'(net_j) x_k \end{split}\]以上,可以看出对隐层的节点权值的求导就更加复杂一些了,因为每个隐层节点的输出$y_j$都是要与上面的每个输出节点$O_i$相连接的,所以对损失函数求关于$w_{jk}$的导数,每个输出$Z_i$都有影响。我们看最后的结果,隐含层权值$w_{jk}$的导数,与上一层的所有节点都有关系(上一个层每个节点的sensitivity ,与该隐层节点对应的权值),与该权值对应的输入层节点(或者隐含层节点)有关系,与当前层的净输入值有关系——好多好多关系。不过只是形式复杂,真正算起来也比较的清晰的。
同样的,对于该隐含层的每个节点,$\sum_{i=1}^c \big ( ~ \delta_i w_{ij} ~ \big ) f’(net_j)$也是相同的,我们将其也定义为sensitivity,即:
\[\begin{equation} \label{hSensitivity} \delta_j = \sum_{i=1}^c \big ( ~ \delta_i w_{ij} ~ \big ) f'(net_j) \end{equation}\]于是该隐层每个权值的梯度可以表示为
\[\begin{equation} \label{hgradient} \frac{\partial J(W)}{\partial w_{jk} } = \delta_j x_k \end{equation}\]由$(\ref{hSensitivity})(\ref{hgradient})$,就可以表示隐含层每个节点中每个权值的梯度了。
想想如果网络有多余1个的隐含层,那么对倒数第二个隐含层中第k个节点中第t个权值,对于损失函数$J(W)$的导数为:
\[\begin{align*} \frac{\partial J(W)}{\partial w_{kt}} &= \sum_{i=1}^m [ \sum_{i=1}^{c} \big ( ~ \frac{\partial J(W)}{\partial Z_i} \frac{\partial Z_i }{\partial net_i } \frac{\partial net_i }{ \partial y_{j} } ~ \big ) \frac{\partial y_j }{\partial net_j } \frac{\partial net_j}{ \partial y_k} ] \frac{\partial y_k}{ \partial net_k} \frac{\partial net_k }{\partial w_{kt}} \\ &=\sum_{i=1}^m \big ( ~ \delta_j w_{jk} ~ \big ) f'(net_k) x_t \end{align*}\]由此看来,后面的隐层与第一个隐层的形式都是相同的了。
梳理一下,我们从求导这个原始的操作中脱离出来。通过求导,我们得到了每层每个节点的“敏感度”(sensitivity),我们先不讨论这个值具体怎么算,反正记住,每个节点中每个权值,都是这个节点的敏感度,乘上这个权值对应的输入的值(对于输出层,输入是下一层对应位置的隐层值,对于隐层节点,则是输入值或者下一个隐层的值)。
再说敏感度怎么算
——对于输出层,就是该节点的输出值与预期值的差,乘上激活函数对净输入值的导数。
——对于隐层的每个节点,就是上一层所有节点的敏感度在该节点中对应该隐层节点的权值,再求和,和值再乘上该隐层节点激活函数对净输入值的导数。
下图说明了backpropagation的过程。