这是《算法分析与设计》课程的实验课部分的内容。这篇文章也是在实验报告的基础上稍稍修改的。这篇文章基本不讲具体的关键算法，而主要讲一些操作的实际实现，以及在实现中所需要注意的细节。

根据实验的要求，分别使用了暴力法，Graham算法以及基于Graham的分治算法。

实验的代码见Github项目：convex_hull

以下内容修改于上交的实验报告。本来想要好好的从头到尾，由整体的关键算法，到细节的问题都写下来，不过最近时间实在紧张，花在这件事情上有些不值得。因为其实代码注释已经写得太详细了…又是Python写的，不必再用说任何伪代码了。至于整体的关键想法，这些网上都是一大堆（除了分治方法，网上的分治都是基于画三角形的。只有咱们讲的是在Graham的基础上做分治 - - . 对了，分治的实现主要受到了以为学长在CSDN上的博客的启发。虽然他的代码根本没有实现分治…不过激起了自己写好它的信心。因为我之前对老师讲的方法是持怀疑态度的——PPT上讲得含糊，而网上也鲜有这么做的），然而细节以及一些我觉得有必要记下来的东西，又都写在了报告里，就全部扔到这里来啦——调格式也比价蛋疼的…

记录下为什么选择Python来写这个实验，以及对于以后遇到类似问题时该如何选择：

1. 从心底来说，我一直是喜欢用C++的，我觉得这样的代码才有感觉。然而我再调研了一段时间C++绘制图形的库，发现除了MFC、QT之外，似乎真的很少有靠谱的图形库了…然而，我根本不需要界面，只需要绘制图。就在我终于艰难的觉得用MFC，然而后来又发现实验要求要绘制性能曲线，我终于放弃了这个想法。

   事实证明，我是对的。

2. 算法的快速实现，请使用Python

   如果我用C++，即使不画图，我觉得自己都不一定能在一周内克服这么多的BUG，写完这两个实验。

   真的遇到了太多的BUG。因为是Python，所以代码上几乎没有任何BUG，所以出现问题，就可以确定肯定是来自逻辑上问题。而Python直接可以Print数组的方法，在平时开来毫无用处，但是关键时刻查找错误却是非常便利的。这个时刻你要用C++，可视化或许好点，能看下内存什么的（有点瞎说，根本没试过），然而基于VIM的开发，找BUG同样只能用打印LOG的方式。而C++在便利性上真的差太多了。

   如果需要专注与算法，那么一定要用Python。

   优雅的代码不在语言，而在逻辑。Python写得烂，同样难以忍受。而C++写得漂亮起来，就真的让人叹为观止。C++本身就是一门艺术，Python则适合用来快速创建艺术。

###生成指定大小、指定范围内的点集合

根据实验要求，需要生成范围为以(0,0)-(100,100)为左上角和右上角的正方形区域内的点，点集合的大小——即点的个数为1000,2000,3000等

我们将点的个数设为参数，所以代码关注于点的生成算法。

既然是点的集合，我认为应该满足：不存在重复点！

此外，在代码中我生成了整数坐标的点。所以100*100的范围，最多点为10,000个，是可以满足要求的。

核心思想是：要随机生成不重复的点，而且要保证概率相等，这个其实是不容易做到的！因为Python语言的方便，同时这里100*100大小可以接受，所以：

1. 我先生成全集——即该区域内全部10,000个点（整数点）

2. 使用随机无放回采样函数sample，从此全集中随机抽出指定数目的点。

可知上述算法能够生成无重复、随机点。

###蛮力法算凸包

虽然网上有相对较优的算法(O(n^3))，不过这里还是按照PPT上的方法使用了O(n^4)的方法。当然，由于在循环中加入了被删除点的跳过操作，实际时间消耗将大大小于O(n^4)（实际上，曾经测试过不加跳过操作来还原暴力法的原貌，但是无奈耗时实在太长，只得放弃）。

接下来说几个关键的地方：

1. 如何判断一个点在三个点围成的三角形中

   这里有个坑，即首先需要判断这三个点能不能构成三角形。后面单独再说。

   按照PPT的方法，就是分别以前三个点中的两个做为一条直线上的点，求解这条直线，算剩余的一个点和待测试点到这条直线的距离（这里指函数距离 functional margin ，当然实际上只需要知道符号），如果二者距离之积为正，那么在同一边。否则不在同一边。如果相对于三个点中任意两个点构成的直线，该测试点都与三个点中剩余一点在同侧，那么则该点在其内部！测试点不是凸包！ 该段逻辑在find_convex_hull_bruteforce.py中，calc_line_params, is_in_same_side, is_3pnts_in_one_line, is_in_rectangle 4个函数中。注释应该比较清晰，不过英文表达可能稍有不畅，关键地方都是用了中文描述。

2. 上述三个点如果在一条直线上该如何处理

   用matplotlib画出暴力法结果时发现了问题，不对！！通过观察log输出，以及对代码逻辑的考虑，发现了上述的问题！PPT上因为是提纲挈领的讲算法，自然不会提及这种细节，但是代码实现上任何一个考虑不周，就会导致BUG。

   如果三个点在一条直线上，那么此时对于待测点是不能够给出是否不是凸包点的结论的！而上述判断算法将给出非凸包的结论。因为按照上述算法，is_in_same_side在其中一个函数距离为0时会返回真。此时因为三点共线，就会认为待测试点全部在同侧（结果全部为0，均返回真），认为是非凸包点。结果错误！

   直观的想法是，判断是直线后，直接跳过此次判断。

   但经过思考后，确定了如下更好的方案：如果三点共线，则必然三点中中间的点不是凸包！！

   以上逻辑很直观，应用凸集合也可以证明。代码逻辑在find_convex_hull_bruteforce.py中的91-95行。

3. 四重循环判断点是否不是凸包

   如PPT上的所述，不赘言。

以上就完成了蛮力法求凸包。比较直观简单，但有坑。

###Graham-Scan算法求凸包

我觉得主要有一下几个关键点

1. 为什么可以这样做

   其实可以用凸集合的图示来想——如果存在右转的点，那么就存在一个内凹的角。在内凹部分的两个极点画一条线，该线在集合外部！所以此时就不是凸包了。

   再，如果是直线呢？即不左转，也不右转——按照凸集合的定义，这个点不是极点。所以不是凸包。当然，我觉得要是认为是凸包吧，或许问题不会很大。但是这里我们严格按照定义。

   所以以凸包上的点为起点，非左转点不是凸包上的点。

   而所有点中y值最小的点，必然是凸包点。（这里表述不是很清楚，后面会更详细的论述）

2. 如何极角排序

   直观的想法，使用余弦角度。$\theta = arc cos<\vec x , \vec p>$，其中$x$向量是极轴，$p$向量是在归一化到极点上的坐标。因为极点是y值最小的，所以所有的点都在一二象限内，此区域内cos是单调递减的。所以余弦值越小，极角越大！由此算出每个向量相对极轴的极角，由小到大排序即可！这里有个坑，就是浮点数的判断。在调试过程中，发现明明极角相同，但是算法给出的结果却不是如此。通过打印log发现，由于cos求值需要算距离，这里涉及到了开平方sqrt操作，结果为浮点数。不相等的两个浮点数，在64位表示下仅仅最后一位不同，然而如果直接使用=判断，就是不等的！于是想起了C语言中判断浮点数相等的方法，只要两个数的差在某个范围内即可认为相等。config.py中的EPSILON常量，即定义了该相等的阈值。

   使用向量的叉乘。我们将二维坐标系中的两个向量扩展到三维，那么原始的$p1 = (x1 ,y1)$ , $p2 = (x2 ,y2)$就可以表示为$p1 = (x1 ,y1 ,z1=0)$ ,$p2 = (x2 ,y2 ,z2 = 0)$，根据向量的叉乘公式，结果为

   \[p1 \times p2 = ( y1z2 - z1y2 ,z1x2 - x1z2 ,x1y2 - y1x2 ) = (0 ,0 ,x1y2 - y1x2 )\]

   叉乘满足右手定则，故只要p1向量的极角大，那么叉乘的结果向量向z的负方向，此时$x1y2 - y1x2$为负；如过$p1$极角小，那么结果为正；如果极角相同，则等于0（由此给出了判断两个向量共线的方法，即上面用到的三点共线的判断）。故直接根据$x1y2 - y1x2$结果的正负，可直接给出两个向量极角的比较。由于使用Python内建的sorted函数排序，只需要定义两个元素的cmp函数即可。此恰恰满足要求。

   find_convex_hull_grahamscan.py中get_polar_angle_cmp_function定义了上述两种比较函数，经过比较，其结果是相同的。但是cos需要开方，运算量明显比较大，且计算结果不够精确。故实际使用时，使用的是基于叉乘的结果。

3. 如果判断左转

   如上描述，直接根据叉乘结果。

4. 如何初始栈中的三个凸包点

   PPT就是简单的将极点、排序后的前两个点放入到栈中即可。然而实际上却远远不止这么简单。

   考虑情景：

   a. 有最小y值的点大于3个

   b. 三个点共线

   a、b情景有所包容，但是b情景包含的情况更多。首先考虑情景1，此时就出现了极点选择的问题——多个最小y值的点，选哪一个呢？经过权衡比较，选择最左边，即x值最小的点最好。此时只要再找到最右端的具有该y值的点，再加上下一个排序后的点，就必然构成了初始凸包中的点！ b情景，首先要去除a中的情景（因为多个y值相同也肯定共线，这里不考虑此情况）。即他们的y值是不同的，不满足a，但是它们就是在一条直线上！这种情景的概率应该是比较小的，但是恰恰被我遇到了…解决办法，就是顺序遍历排序后的点，直到找到不共线的即可。

5. Graham-Scan算法

   如PPT上所言，不赘述。

###分治法

关键点有两个，我认为是PPT讲的比较含糊的地方：

1. 到底如何合并

   首先，如PPT上画的图，选择的新极点是左边凸包的内点。所谓内点，就是凸包内部的点。根据凸集合的定义，所有内点都可以根据凸包点线性插值表示（具体实现见find_convex_hull_dc.py中generate_inner_pnt函数）。 因为是内点，所以左边的整个凸包对于该点都是逆时针有序的！

   考虑右边的凸集合。首先，右边的集合已经是一个凸包了，所以所有的点必然也是相对于其内部点逆时针排序的！但是，相对于左边的点，他们就不是有序的了。但我们可以找到右边凸包点中，相对于左边极点，极角最大和最小的点。那么由最小的点到最大的点，逆时针遍历右半部分，得到的序列对于此左边极点是逆时针有序的；对于左半部分，顺时针遍历，得到的点序列相对此极点是逆时针有序的。这个可以画一个图，能够比较直观的看出。证明不是很会。上述时间复杂度是O(n)（代码中使用了算法导论以及PPT上都提及的使用分治找最大最小值的算法，比价次数是3n/2，当然，时间复杂度仍然是O(n)）。 现在我们就得到了三个相对于同一个极点分别内部有序的序列了！直接对这三个序列做关于此极角的Merge排序，使用上面定义的比较函数即可。时间复杂度是O(n)。 以上，就完成了Merge操作。

2. 分

   PPT上给出的话一笔带过。实现时为了达到真正有意义的分治算法，使用了线性时间查找中位数的方法。即实现了《算法导论》第九章中第i顺序统计量中，randomized_select算法。

   成功找到了中位数，但是划分时出现了BUG。假设我们将小于等于中位数的点划到左部分，其余到右部分。同样考虑两种情景：

   1. 所有点的x值都相同

   2. 找到的中位数实际上是所有点中x值最大的

   上述情景b发生的概率较大！上面任何一种情况，都将导致左部分子集为待划分集合，而右部分为空！这样递归调用，将无穷递归！最终爆栈。

   解决办法比价简单，第一种情况直接分成两半，第二种就改变逻辑，将小于中位数的划到左边，大于等于的放到右边。

   非常多的细节。不再赘述。代码见find_convex_hull_dc.py

###实验结果（运行结果截图）及对比分析（时间性能曲线）

控制台输出（最后为时间，单位为秒）：

得到的凸包图示：

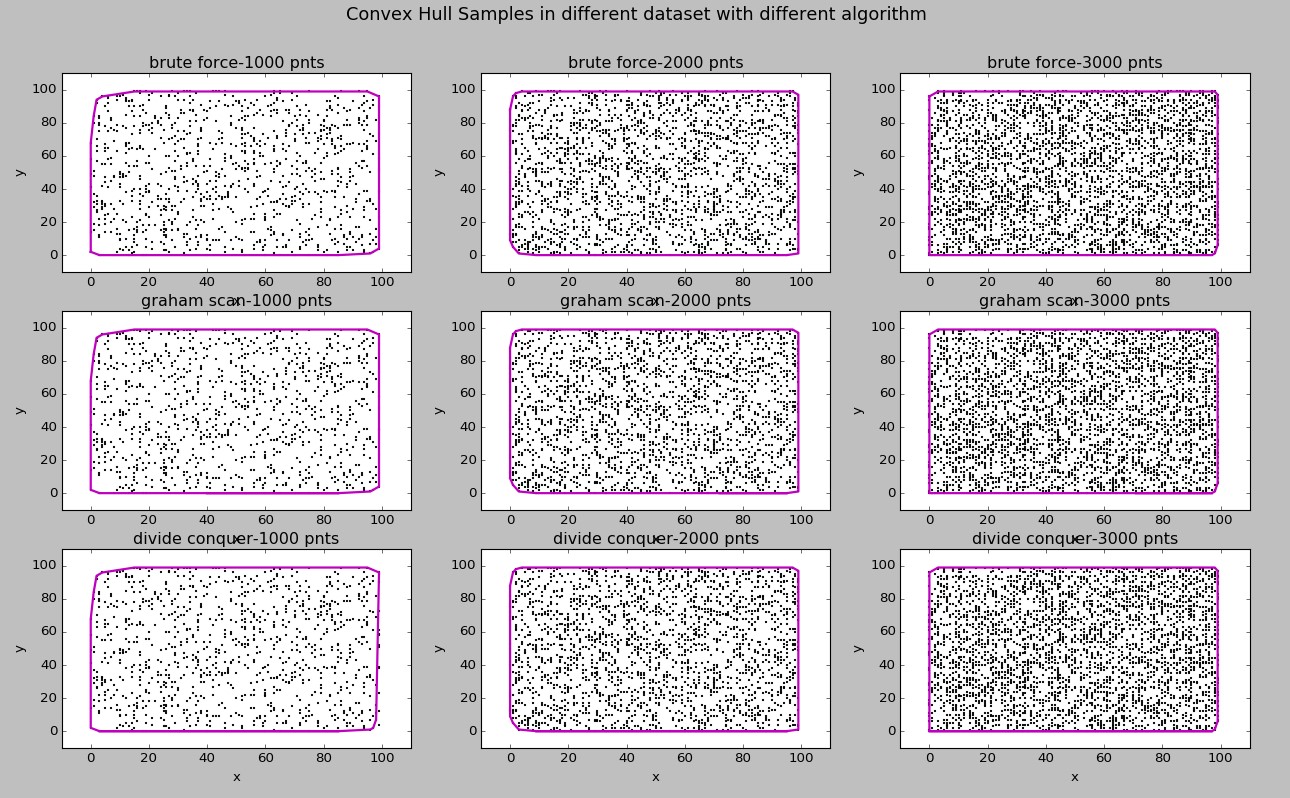
根据时间消耗绘制的性能曲线图：

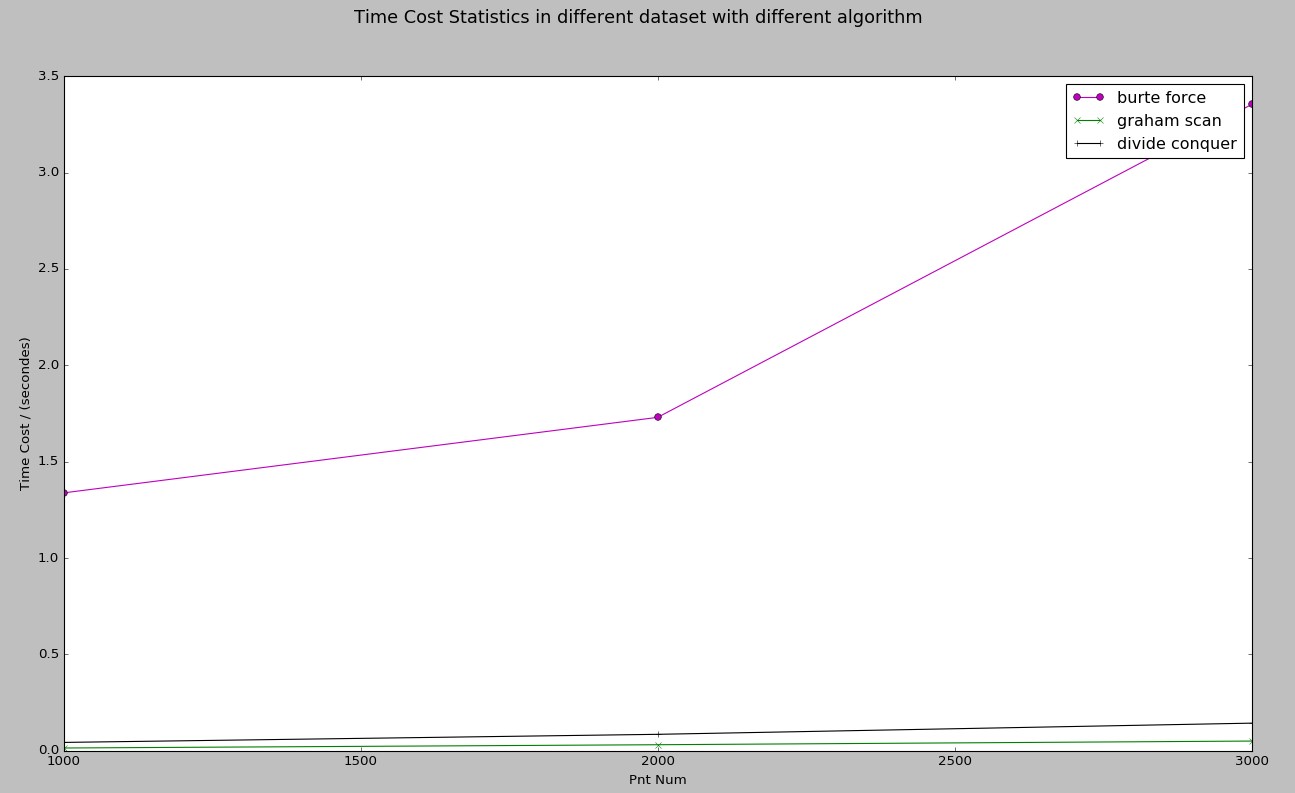
由上面的图可以得到如下结果：

1. 所有算法实现正确。根据算法找到的凸包点的确是凸包点。

2. Graham-Scan时间耗时最少。分治次之，暴力太慢。

分析1：为何分治比Graham慢？

尽管时间复杂度都是O(n log n )，但是通过算法描述，的确可以知道，分治方法比较复杂，一些操作开销比较大。具体来说：

1. 每次划分数据集，要生成子集。在Python实现中，直接使用了生成式来完成。相当于又申请了内存。而内存申请与释放都是耗时的。

2. 递归操作。递归是耗时的，因为要保持当前的程序状态，涉及到大量程序现场的保存，弹栈出栈消耗大。

而Graham是没有上面的时间消耗的！

分析2：暴力法似乎并不是O(n^4)的？

因为在循环操作中，对已经判断出的不是凸包的点，直接跳过了判断。首先，这对程序的正确性没有影响！因为不用依靠内点去消除内点——凸包点可以完成此任务。然而，它大大减少了迭代、计算次数。曾经测试过不加此跳过超过，其时间消耗难以忍受。

###实验心得

1. 工程实现需要考虑大量细节

   在上面的实验过程及结果中已经说明了大量的细节。比如需要判断三点是否共线、判断按中位数划分左右子集是否真的成功、Graham初始栈中的三个元素需要一段精心的考虑等。而这些，在算法描述中都是忽略的。算法描述的是最关键算法的思想，严谨的伪代码可能会考虑到下标等，但是也绝不会精细的处理每一个细节。 所以，不真的把代码写出来，不能说真的了解了一个问题的实际解决方案。

2. 精妙的算法以及数学

   使用Graham-Scan算法，就能够如此效果显著的降低时间复杂度，不得不叹服算法的强大。

   而向量的叉乘，就能知道哪个向量的极角大、是否共线等，真是神奇。

3. 有BUG不能怪数据

   因为使用的是整数点，所以写的过程中发现了大量的BUG。在暴力法判断凸包时，发现结果竟然不对，当时内心是崩溃的…知道是共线问题，但是如果加判断，最简单的暴力也变得复杂了。当时把生成点的方法改成随机浮点，结果就正确了。后来还是觉得，墨菲定律需要引起重视——凡是可能出错的，必然会出错。其实也是幸运，能够快速找到引起错误的Case。最难调的Bug，不就是小概率时出现的Bug吗?既然是幸运的，那就老老实实改代码咯。