本文基于《算法分析与设计》的实验二写成。

实验的代码见Github项目：hamiltonian

续上篇。由于写得太长了，分成两篇来记。以下也是报告内容的复制。

###生成无向连通图；生成加权无向完全图。

生成无向连通图，给定端点数N，于是设端点就是0,1,…,N-1 , 边直接用邻接矩阵表示。由于是无向图，邻接矩阵必须是对称矩阵，且对角线上元素为正无穷。由于必须生成连通图，而依靠概率决定是否有边并不能保证其是连通的，故先随机出一条连通边。然而再在此基础上随机添加边。随机连通边的生成算法：将端点列表随机打乱(shuffle)，按序每次输出两个，就是一个随机的连通路径。代码为项目文件夹（hamiltonian）下文件generate_random_connected_graph.py中的25-30行。

生成加权无向连通图，就是随机权值即可。同样保证满足对称矩阵。代码为generate_random_connected_graph.py中的44-48行。

###构建“状态”结构来存储遍历时的状态

代码见state.py中StateMemoryLess类、State类。

每次遍历，我们将状态保存到栈或队列中，下次从栈或队列中取出时再读取状态来保证遍历的可行性。 BFS、DFS、HillClimbing算法由于不需要改变邻接矩阵，就构建了StateMemoryLess类，仅保存当前的各节点的访问状态，当前的节点ID，以及到达当前的路径（为了返回最终的哈密顿路径），此外，为了方便，还记录了前一个节点（其实这里可以直接通过路径来得到，这么看来似乎有些冗余。当时是开始时没有准备加入路径的支持，因为程序仅要求输出是否有哈密顿环，而不必要返回路径。但是后来考虑到要画图，就增加了路径的支持，原始的逻辑也就没有变了）。

分支界限法由于每个状态的代价矩阵是不同的，所以增加了代价矩阵这一属性。同时，用low_bound来表示扩展到当前状态所需要的最小代价（即每行、每列减去一个值使得每行、每列至少有一个零，这些减去值的和）。同时，定义了in_mask和out_mask这两个结构，来表示那些节点的出度、入度连接已经被占用了。定义了一系列操作来帮助分支界限法更方便的操作，主要有normalize_cost_matrix_and_update_low_bound及单独操作行、列的函数，用来做上述每行、每列减去一个数使得每行每列至少一个零的操作，并自动改变low_bound值。函数select_one_edge_to_minimize_left_subtree_and_maximum_right_subtrue定义了从代价矩阵中，选择哪一个（i,j）边，使得左子树代价下界增加为最小（为0）而右子树代价增加最大（即PPT中的f(i,j)功能）。check_graph_state函数来确定当前状态，是否已经有哈密顿环，或者已经有了局部环、亦或者还可以继续扩展。注意，这个函数并不能判断是否应该被剪枝。剪枝操作是在分支界限法中完成的。

###DFS 深度优先搜索

算法思想如PPT上所言，使用栈来保持状态，深度优先找到一个解。我觉得需要注意的地方是，如何进行扩展以及是否已经有哈密顿环的判断。

我的方法是，在每个状态给出其可以扩展到的所有合法节点（在StateMemoryLess类中实现）。合法节点满足以下条件:

a. 节点没有被访问

b. 节点可达

（代码中似乎还加了一个，非父节点，现在看似乎有些多余。因为条件a已经包含此情景了）如果有可达节点，那么必然此时没有哈密顿环——因为嗨哟与节点没有被访问。否则，则该节点已经不能再进行扩展了。此时，就需要检查是否有哈密顿环了。检查哈密顿环的操作同样在StateMemoryLess中实现，首先看所有节点是否被访问，且该节点是否有到起始节点的边。 如果是，则返回该环，注意在路径中的末尾再加入一次起始节点，作为环。否则就继续遍历。当栈中为空时还没有找到，则没有，返回None.

DFS的代码文件为：dfs.py

###BFS 广度优先搜索

原理与PPT上所言，不再赘述。实际实现时，除了将DFS中的栈改为队列，改变相应的操作函数外，完全一致。故不必多言。

BFS的代码文件为: bfs.py

###爬山法

整体搜索构架与DFS完全一致。增加的逻辑就是将各状态入栈的顺序！开始猜测的启发式规则如下定义：

1. 选 有最多的连通、未被访问的节点数 的子节点

2. 在1的基础上，若相同，则选择有最多连通数的子节点

设计一个启发式打分函数：

分数 = 连通且未被访问的节点数 * 节点数 + 连通但已经被访问过的节点数

前一个量乘上节点数，是为了强制使得第一个量为 关键因子！ 在此条件下，应该只有在第一个量相同时，才会考虑第二量。因为前一个量每次增量是大于等于后一个分量的最大值的，直观的可以证明，只要第一个量大，那么它的分数一定大，而与第二个量无关！

然而经过实践，发现上述规则是错误，而且恰恰相反！

于是我将上述打分函数取反，发现效果真的叫DFS在大多数情况下优异！关于此结论，想到的一个可能解释是：连接的点越少，可能有较大概率是一条关键路径。即如果有哈密顿环，那么此边更有可能在哈密顿环上，因为到达该点的路径少！这么一想似乎也是很有道理的…

###分支界限法

写得非常难受的代码。调试了一天，终于豁然开朗了。PPT上只是讲了怎么做，但是并没有讲为什么可以这么做。同时，代码实现上的细节问题，如当代价矩阵全是无穷大时怎么办让人困惑。可能是当时上课没有好好听课吧…

自己对于这个代价矩阵每次保证至少每行每列有一个0，且扩展的最低代价就是减去的值的和（这里的最低代价不是指哈密顿环的代价下界，而是指扩展到该状态时的代价下界。如果此状态是一个哈密顿环，才可能是哈密顿环的下界。不知道今天有没有给助教解释清楚…）这一结论的理解：每行减去的值，就是从该行索引对应的节点，出去所需要的代价。每列减去的值，就是进入到该列索引对应的节点所需要的代价。而减去后的代价矩阵，表示在上述出去、进入的代价之外，在路程上的代价。由于一个哈密顿环，每个顶点都必然要进去一次、出去一次（无向图来说，就是度为2），所以哈密顿环的最小代价就是减去的这些值的和。以上就是我的理解。

至于代价矩阵中的值全为无穷大的情况，其实是无不可能存在的，因为在种情况下，肯定已经被剪枝了。

具体来说（如PPT上所言）：每次找到每行中代价矩阵为零的元素，且使得除去该为0元素后，该行的最小值、该列的最小值的和在所有满足条件的行列中最大（这段逻辑的实现为State类中的select_one_edge_to_minimize_left_subtree_and_maximum_right_subtrue）。找到该元素后，构建左子树和右子树。左子树是将该元素对应的行列删除（实际代码实现时，将in_mask , out_mask对应下标位置的值设为True，其中in_mask指列，out_mask指行，原因如前面的理解），同时将(列、行)元素的代价值设为无穷，再归一化代价矩阵并更新low_bound(所谓归一化，就是指保持每行、每列至少一个0。这段代码见：State类中normalize_cost_matrix_and_update_low_bound)。右子树，只需将该元素的代价值设为无穷，再归一化矩阵，更新权值。注意，此时，就需要进行剪枝操作（对应代码为：branch_and_bound.py中77-80行）。再未被剪枝的情况下，先压入右子树，再压入左子树。保证左子树优先扩展。

在访问每个状态时，需要检查此状态：

1. 是否已经是哈密顿环，如果是，此时状态的low_bound就是此哈密顿环的代价，与全局最小的代价比较，如果小就记录下来，并记录此时的路径。

2. 是否已存在非哈密顿环。即PPT上“注意”中的情况。此时抛弃该状态即可。

3. 否则就是正常状态，继续扩展左右子树。

上述逻辑见代码：branch_and_bound.py中27-42行。当栈中为空时，即返回找到的最小代价对应的路径，即最小哈密顿环。 由此即完成了分支界限法。代码文件：branch_and_bound.py

###算法运行结果截图及算法性能曲线图

控制台输出（部分）

包含日志输入，以及各方法的路径输出。

时间消耗（控制台输出）

顶点数为8、10、12时BFS、DFS、爬上法找到的哈密顿环（由于屏幕限制，更多点的情况没有绘制出来）

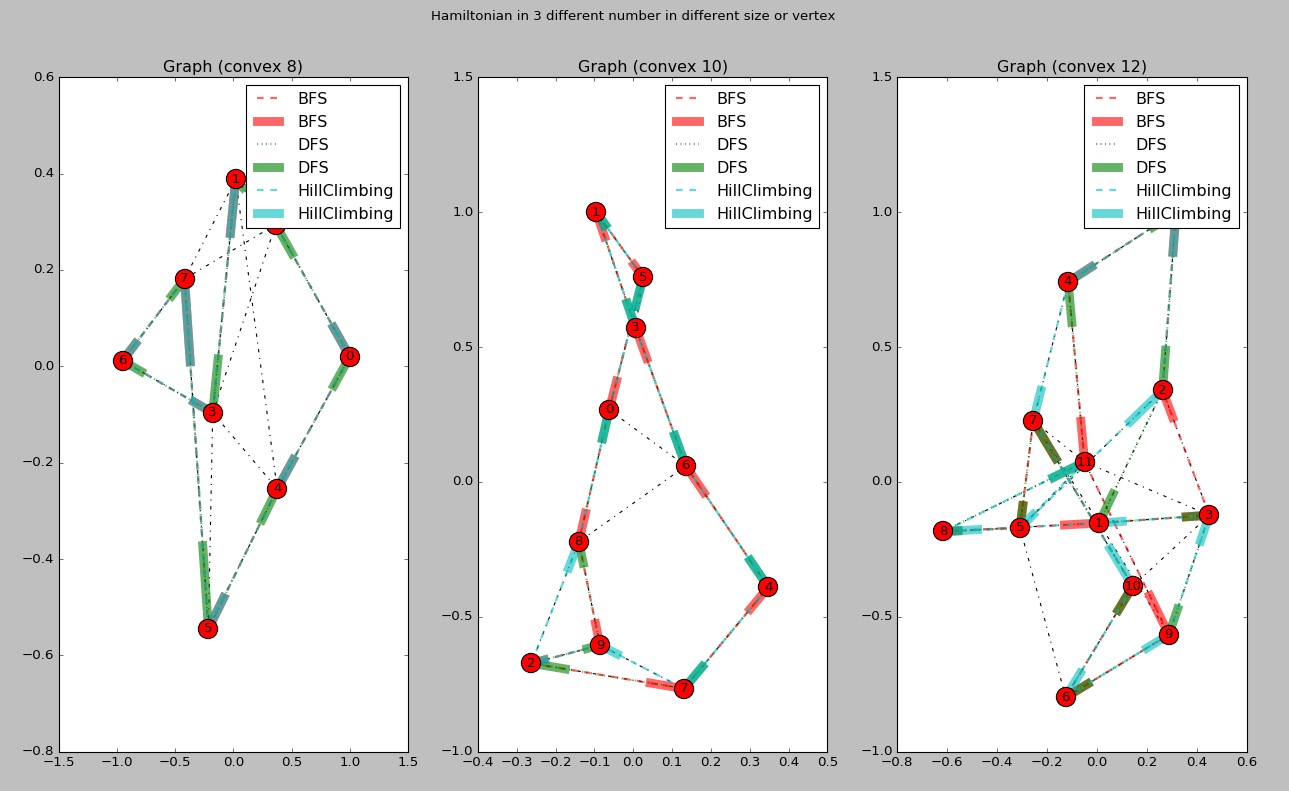
环使用有向边表示，粗边表示箭头。虚线表示图中的边。各颜色的有向边表示各方法求得的哈密顿路径。

顶点为8、10、12的最小哈密顿环绘制（同样由于屏幕限制更多的顶点结果没有绘制。）

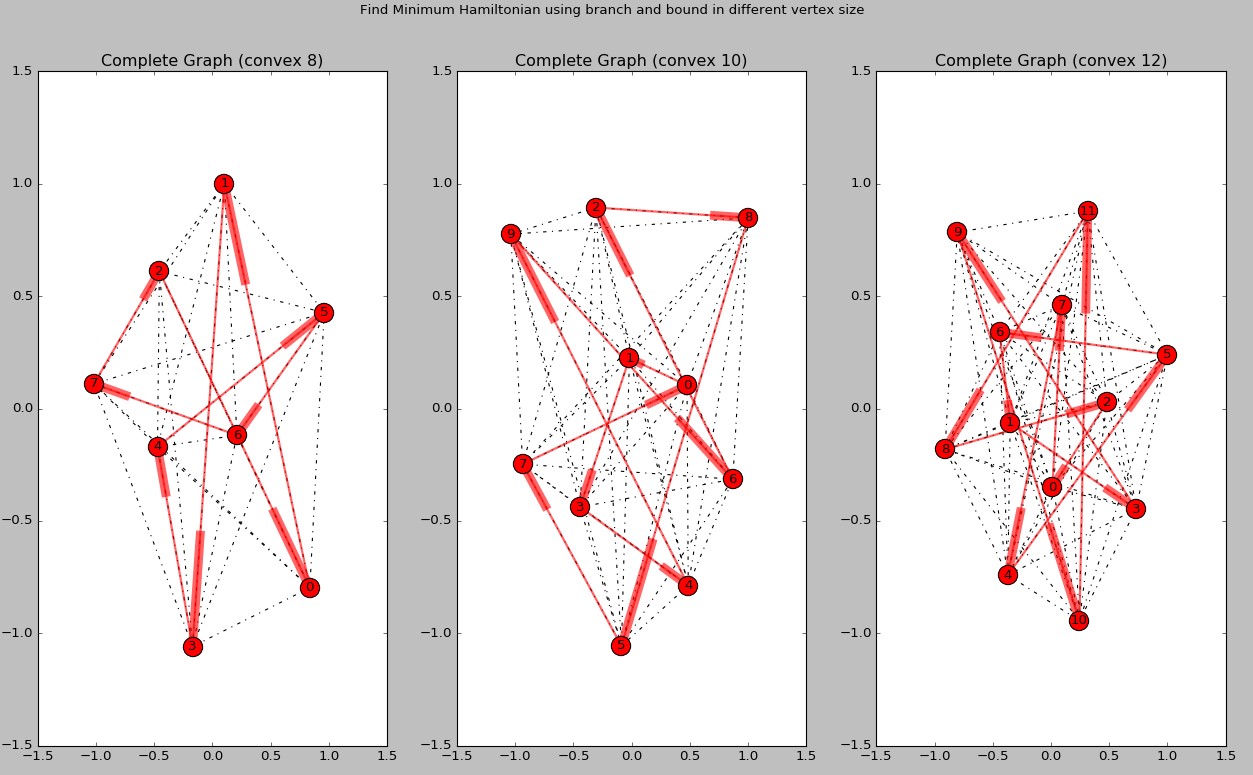
虚线表示完全图的边。路径也使用有向边表示。

BFS、DFS、爬上法的性能曲线

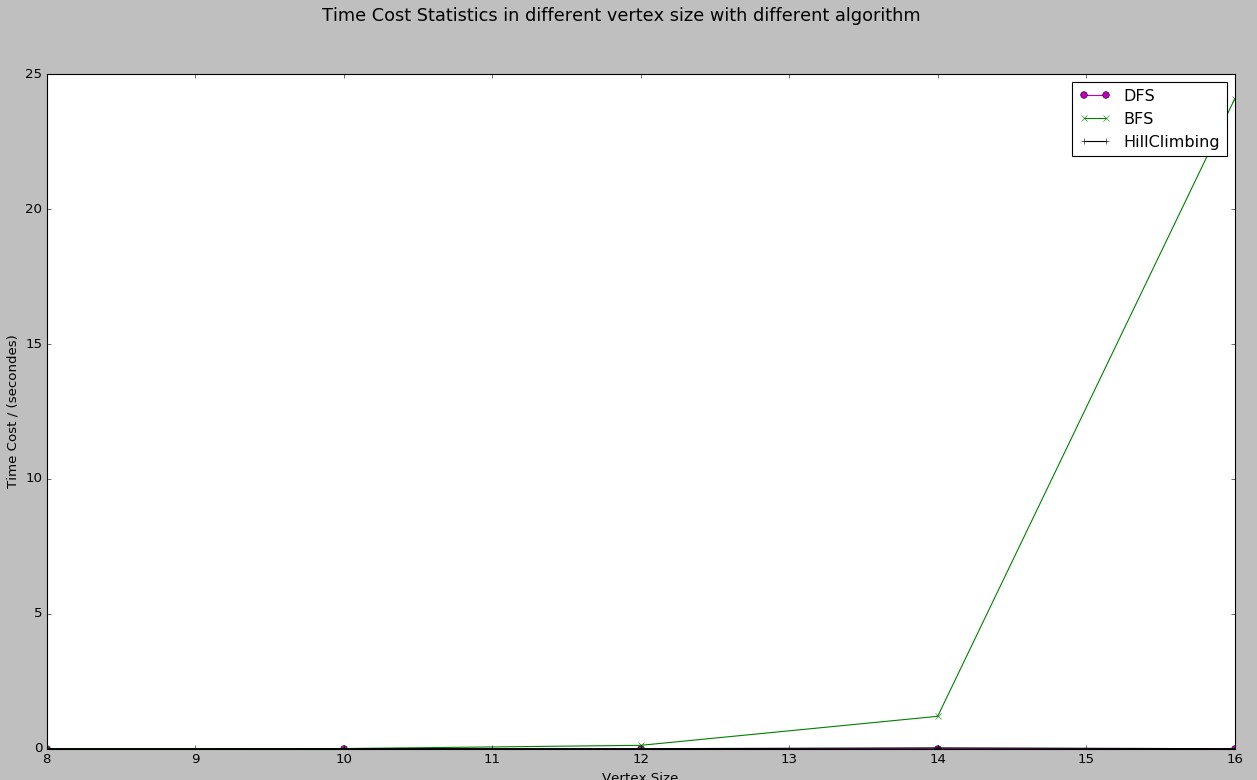
由于DFS、爬山法时间消耗太少，而BFS消耗太大，故前两种方法的曲线接近于0。（由于matplotlib不能直接在图上显示时间消耗的具体值，故图上没有标志。但可以查看上面控制台的输出。图的绘制即是基于上述数据。）

找最小哈密顿环的性能曲线

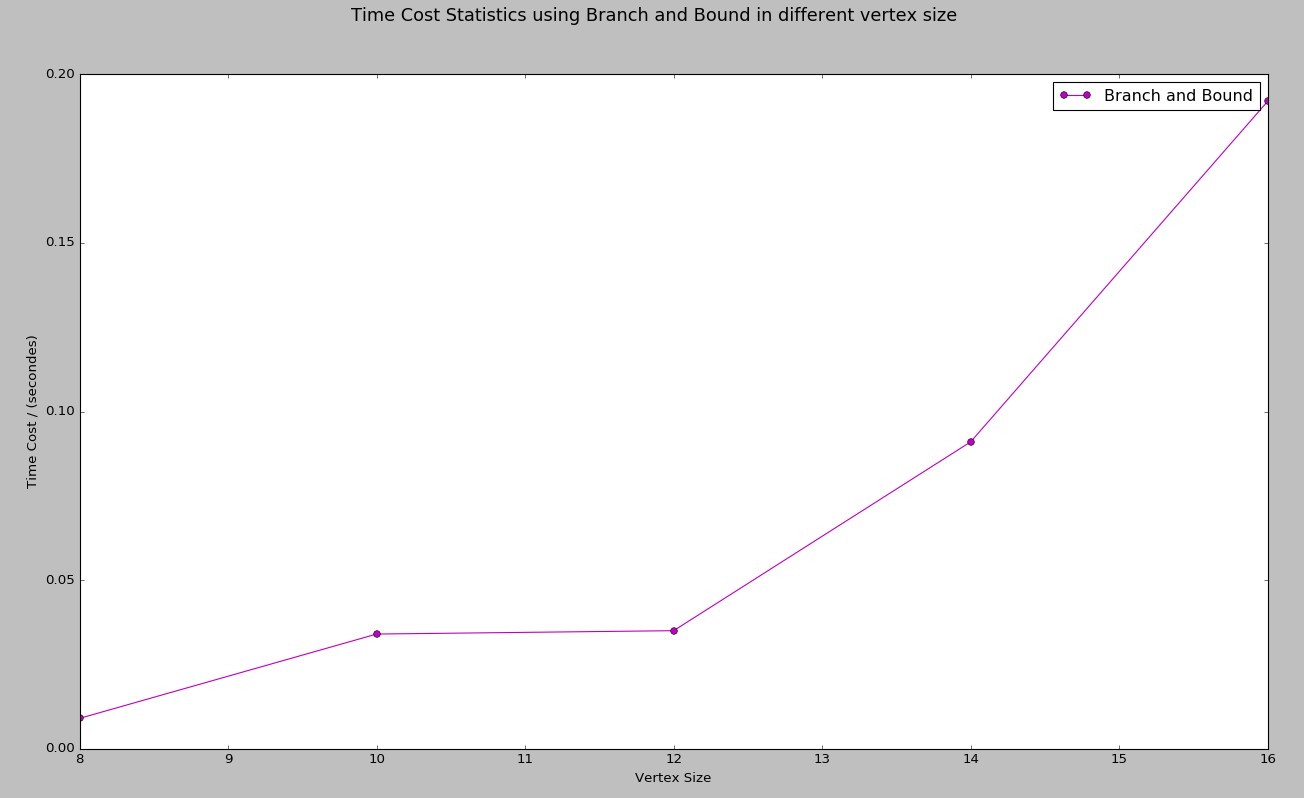
同样，时间可以查看上述控制台输出。

注： 上述顶点均只计算到16个点，18、20这两种情况均未计算。因为BFS实在太耗资源，而本机PC 8G内存也显得捉襟见肘。

1. 结果分析

2. BFS太耗资源

   在找存在哈密顿环的情况下，使用BFS实在不是一个明智的原则。因为使用队列，所以每次都要扩展整个连接的节点，且下次继续扩展。设有N个节点，则第一次扩展队列有N-1个节点，该N-1个节点扩展完，有(N-2)^(N-1)这么多个，如此这么多个再扩展，数量将呈指数爆炸。

3. 爬山法效果不错，但此情景下时间消耗仍然高于简单DFS

   首先要明确为何时间消耗增加—— 一种可能是，启发式规则不对，导致其相对随机的深度遍历（即DFS）反而效果不佳。这个假设一定概率是不对的的，如前面启发式规则那里所言，经过测试，其在大多数情况下是由于普通DFS的。测试方法是通过记录栈操作次数（由于代码在写成后将这段测试代码删除了，故这里不能再提供截图）。多次操作，发现爬山法在上述启发式规则下栈操作次数更少，说明此启发式规则的确减少了遍历的次数（不能完全坑定，但至少是有较大概率的）。另一种可能，就是对状态打分排序的额外消耗了。因为爬山法涉及到对所有状态的打分及排序，故总体耗时会有所增加，这是肯定的。

所以，究竟是启发式规则带来的增益大，还是引入启发式规则导致打分排序其带来的额外开销更大，就要视具体问题而定了。这也是一个Trade-Off.

###实验心得

1. 实践出真知

   当然也不一定准确啦，不过真的去实现你的想法，才能验证你的想法是不是对的。

   在设计爬上法的启发式规则时，刚开始想的是找那些含有未访问节点数最多的子节点，但最后的实验结果却恰恰相反！

   PPT上的分支界限法完全不知道为何要这么做，通过写代码，逼着自己想为什么要这么做，这么做的终结条件是什么，会出现什么样的状态等等。老实说，写完代码，也不能说就彻底懂了，然而如果不写代码，这个方法真的是完全看不懂的！之前一直觉得基于爬山法的分支界限和这种代价矩阵变换的二叉划分子空间的分支界限法简直就是两个东西。现在看来其实本质是相同的——每次找优先遍历最小代价的路径，先去找到一个解。只是代价矩阵方法的感觉是用了全局信息（全局的代价矩阵），应该不适合8-puzzle问题吧。所以感觉此种分支界限法只是一种情况下的特例，而且是特殊解法…就像以前做数学题时那种快速又难懂的方法…