本节讲了相机模型(针孔、畸变、双目、RGB-D)、图像在计算机中的表示及 OpenCV 对图片的基础操作。
1. 术语表
| 中文名称 | 英文名称 |
|---|---|
| 针孔相机 | pinhole camera |
| 齐次坐标 | homogeneous coordinates |
| 内参 | intrinsics |
| 外参 | extrinsics |
| 光轴 | optical axis |
| 主点 | principal point |
| 像素 | pixel |
| 畸变 | distortion/distort |
| 径向畸变 | radial distortion |
| 切向畸变 | tangential distortion |
| 桶形畸变 | barrel distortion (i.e. negative radial distortion) |
| 枕形畸变 | pincusion distortion (i.e. positive radial distotion) |
| 畸变校正 | undistort |
| 相机标定 | camera calibration |
2. 相机模型
强烈建议先看 从零开始一起学习SLAM | 相机成像模型, 易懂、干货多!
(数码)相机模型,描述了一个真实世界的物体变成图像(像素)的过程。一般涉及刚体(点)在 3 个坐标系上的转换:
\[\rm 世界坐标系(P_w) \rightarrow 相机坐标系(P_c) \rightarrow 像素坐标系(p)\]世界坐标系,就是我们建图(slam中的 Mapping )的坐标系。
相机坐标系,以相机光心为坐标原点,光心所在平面为x、y轴所在平面,z轴垂直此平面指向物体方向。 此坐标系下有几个关键的平面:
-
真实成像平面:图像传感器所在的平面,Z轴坐标为负。物体经过光心在真实成像平面成倒立像。
-
对称成像平面:真实成像平面关于光心的对称平面,Z轴坐标为正,且为正立像。有时为运算方便,直接将此平面作为成像平面。
-
归一化成像平面:$Z$ 轴坐标为 1 的点构成的平面。计算畸变时需要用到此平面。
像素坐标系,是一个 2D 坐标系,描述图片或传感器上的像素位置。左上角为原点,横向右为 $u$ 轴正半轴(图宽),垂直向下为 $v$ 轴正半轴(图高)。
ch5 首先介绍最基础的单目、不带畸变的针孔相机模型建模过程,然后引入畸变因素,从而用公式描述了上述过程; 接着介绍双目相机模型,用于求解单目丢失的深度($Z$)值;最后简单说了下RGB-D相机模型。
2.1 针孔相机模型
针孔相机模型核心包含光学层面的小孔成像,以及两个坐标变换,需要求解外参、内参两大类参数。下图大致描述了此过程:
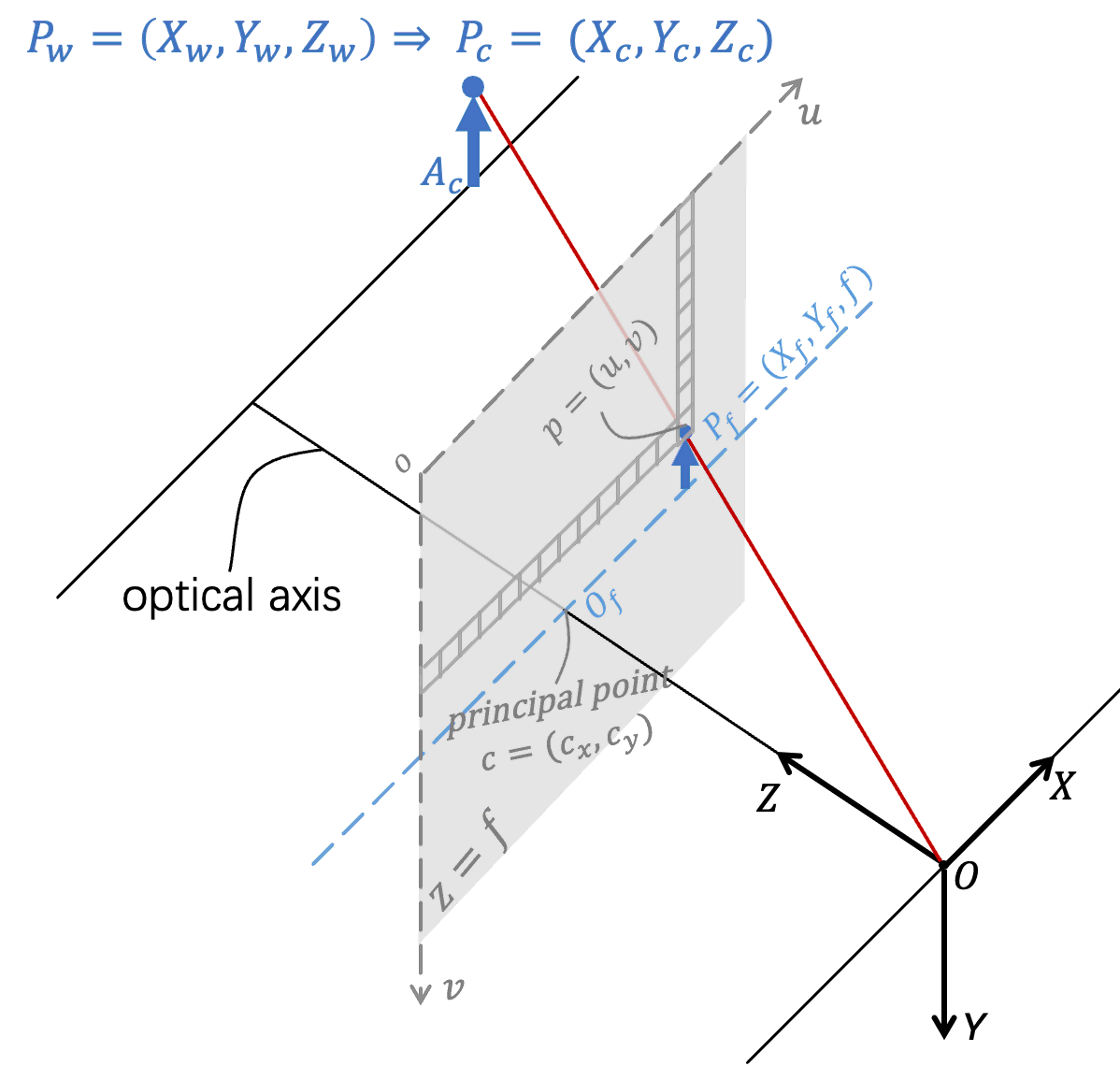
图1: 针孔相机模型
该图基于 opencv-calibration 中针孔相机模型图,结合书上符号绘制。
形式化描述如下:
-
第一个坐标转换: 计算世界坐标系下的点 $P_w = (X_w, Y_w, Z_w)$ 变换到相机坐标系下的点 $P_c = (X_c, Y_c, Z_c)$
点没变,只是坐标系换了。这对应到一个旋转、平移变换(第三讲内容)。
\[\rm P_c = RP_w + t \Rightarrow P_c = TP_w\]$T$ 是我们要求解的参数,也被称为外参.
-
小孔成像: 计算 $P_c = (X_c, Y_c, Z_c)$ 落在对称成像平面($Z = f$)上的点 $P_f = (X_f, Y_f, f)$
对照上图,因为在同一个坐标系下,且针孔相机模型下光透过小孔沿直线传播,故 $P_f$ 就是$\vec{OP_c}$ 与对称成像平面的交点。 故向量 $\vec{OP_f}$ 只需由 $\vec{OP_c}$ 经过简单的常量缩放即可得到。 而缩放常量就是二者 $Z$ 轴坐标的比值 $\frac{f}{Z_c}$. 由此,有
\[P_f = \frac{f}{Z_c} P_c = \frac{f}{Z_c}\begin{pmatrix} X_c \\ Y_c \\ Z_c \end{pmatrix}\] -
第二个坐标转换: 计算 $P_f = (X_f, Y_f, f)$ 转换到像素平面的坐标 $p = (u, v)$
这是模拟量(光)到数值量(像素)的转化。空间中的点转换后到一个平面,$P_f$ 的 $Z$ 轴信息被丢掉了,但计算时还是要用到的!
$P_f$ 坐标的单位是
mm等距离单位,而 $p$ 的单位是像素。前者转换到后者,需要采样和缩放。 在数学上,就是要乘上一个单位类似pixel/mm的缩放系数。我们常听到的 PPI (Pixels Per Inch) 就属于这类缩放系数。特别地,X轴和Y轴的缩放系数一般不同,这里分别记为 $\alpha$, $\beta$.
为何缩放系数不同,下面有简单的猜测。后续我们也看到,其实fx, fy 大部分情况还是挺接近的,且有时即使不同,也可以设置为相同(高博ch7的代码里,fx = 520.9, fy = 521.0, 但在调用
cv::findEssentialMat时,用的是统一 focal = 521)。相机坐标系原点 $O$ 沿光轴方向(即 $Z$ 轴)落在像素平面的点不再是像素坐标系原点,而是叫主点1。 像素坐标系的坐标原点 $o$ 在平面左上角,而主点 $c$ 理想情况下应该在像素平面的中心(所以也叫 image center),然而实际情况并非总是如此, 这里或许有工程安装对不准位置的原因。因此 $c = (c_x, c_y)$ 也是一个需要求解的量.
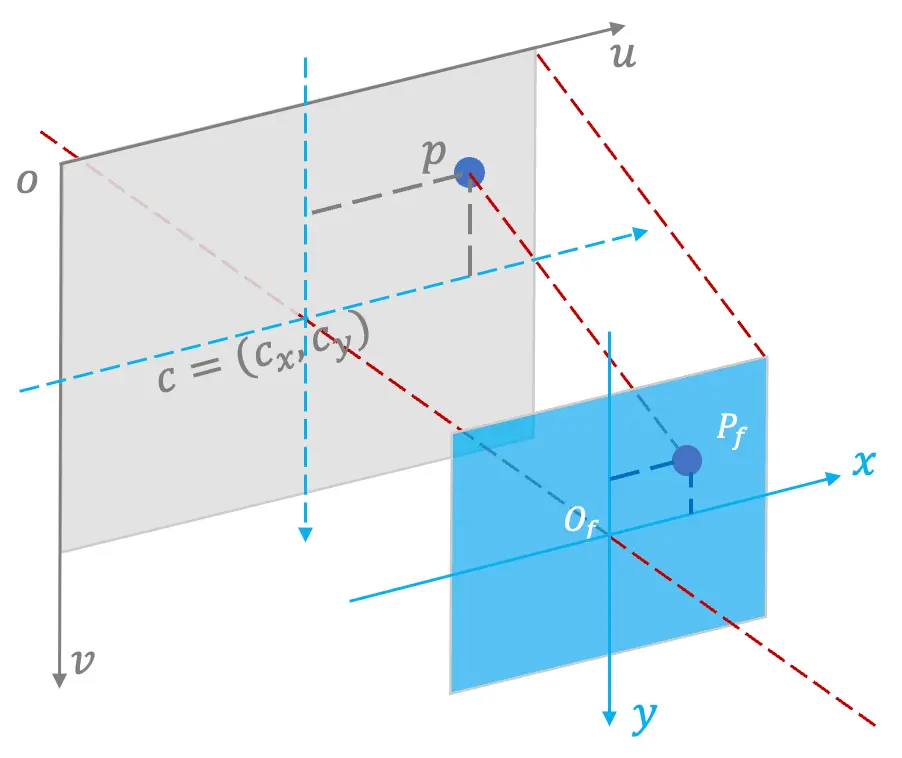
图2:对称成像平面的点落到像素平面
由上图,对称成像平面的原点 $O_f$ 与像素平面主点 $c$ 对应,$P_f$ 横、纵坐标经 $\alpha$, $\beta$ 缩放后落到 $p$ 点, 则 $\vec{cp} = (\alpha X_f, \beta Y_f)$. 又 $\vec{oc} = (c_x, c_y)$, 则 $\vec{op} = \vec{oc} + \vec{cp} = (\alpha X_f + c_x, \beta Y_f + c_y)$, 也即 $p$ 的坐标。 写作矩阵形式,为:
\[p = \begin{pmatrix}\alpha & 0 \\ 0 & \beta \end{pmatrix} \begin{pmatrix} X_f \\ Y_f \end{pmatrix} + \begin{pmatrix}c_x \\ c_y\end{pmatrix}\]
将2、3步骤合起来,则从相机坐标系下的 $P_c$ 到像素坐标系的 $p$, 公式为:
\[p = \begin{pmatrix}\alpha \frac{f}{Z_c} & 0 \\ 0 & \beta \frac{f}{Z_c} \end{pmatrix} \begin{pmatrix} X_c \\ Y_c \end{pmatrix} + \begin{pmatrix}c_x \\ c_y\end{pmatrix}\]令 $f_x = \alpha f$, $f_y = \beta f$, 且引入齐次坐标,可以得到如下简洁形式:
\[\begin{pmatrix} \boldsymbol{p} \\ 1 \end{pmatrix} = \frac{1}{Z_c} \begin{pmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{pmatrix} P_c = \frac{1}{Z_c} K P_c \tag{1. 针孔相机模型公式}\]可以看到 $K$ 与点 $P_c$ 无关,其只与相机自身(焦距 $f$,像素平面横纵缩放比例 $\alpha, \beta$ 和主点坐标 $c$)相关, 故称 $K$ 为内参。
外参将点从世界坐标系转到相机坐标系,对应第一个坐标变换,其随相机位姿变化而变化; 内参再将点转到像素平面,对应小孔成像+第二个坐标变换,相机设置不变则内参保持不变。
求解相机外参 $T$ 是整个 vslam 的关键,将在后续学习。 求解相机的内参 $K$,称为相机标定。书上提到了比较著名的张正友标定法,使用打印出的棋盘格就可以标定出内参。 OpenCV Python 版有标定的Tutorial, 并附带示例的棋盘格图片。
2.2 畸变模型
基于小孔成像的针孔相机在现实中并未大量应用,vslam使用的是基于镜头(lens)的相机。引入透镜之后,光路就不是直线了,成像会有畸变。 影响较大的畸变主要的有2种:
-
径向畸变:以镜片中心为圆心,相同半径上的光折射率一致,但不同半径上折射率不同,整个畸变沿径向方向,故称为径向畸变。
若成像中心膨胀(文献中称中心部分的放大率大于边缘部分放大率),则是桶形畸变。反之边缘膨胀,就是枕形畸变。 桶形畸变常发生在广角镜头,而枕形畸变在长焦镜头中常见。
-
切向畸变:因为图像传感器和光轴没有垂直导致的。
两种畸变对成像位置的直观影响,可参看在透镜畸变与相机标定中的图。
引入畸变后,成像过程和针孔相机模型有哪些差异呢? 变化只在计算 $P_c \rightarrow P_f$ 的部分——即原来基于光沿直线传播的小孔成像模型,要改为畸变模型。其余部分都是不变的。
畸变模型过程如下:
-
将 $P_c$ 映射到归一化平面 $Z = 1$ 上,得到归一化坐标 $P_n = (X_n, Y_n, 1)$.
坐标值除以$Z_c$即可: $P_n = \frac{1}{Z_c} P_c$.
-
在归一化平面上,带入畸变公式计算畸变后的点位置 $P_d = (X_d, Y_d, 1)$
$Z$ 已经为1,我们从平面视角就只关注 $(X_n, Y_n)$ 了。 径向畸变与圆有关,所以要先计算点到圆心(即坐标原点)的距离 $R_n = \sqrt{X_n^2 + Y_n^2}$. 然后有公式如下:
-
径向畸变后的点 $P_d$ 坐标:
\[\begin{cases} \rm X_d = X_n(1 + k_1R_n^2 + k_2R_n^4 + k_3R_n^6) \\ \rm Y_d = Y_n(1 + k_1R_n^2 + k_2R_n^4 + k_3R_n^6) \end{cases}.\] -
叠加切向畸变后点 $P_d$ 坐标:
\[\begin{cases} \rm X_d \mathrel{+}= 2p_1X_nY_n + p_2(R_n^2 + 2X_n^2) \\ \rm Y_d \mathrel{+}= p_1(R_n^2 + 2Y_n^2) + 2p_2X_nY_n \end{cases}.\]
记上述公式为畸变函数为
\[\newcommand{\distort}{\operatorname{distort}} \distort: (P_n \| k_1, k_2, k_3, p_1, p_2) \rightarrow P_d \tag{2. 畸变坐标计算}\]书上直接给出了消除上述两种畸变的算法,但没有提及算法名字。搜索了下,这个算法应该是 Brown-Conrady model2.
-
-
将 $P_d$ 视作之前的 $P_c$, 应用小孔成像+像素坐标转换步骤,得到 $p$
\[\begin{pmatrix} \boldsymbol{p} \\ 1 \end{pmatrix} = \frac{1}{Z_d} K P_d = K P_d\]注意到 $Z_d = 1$.
我们可以把上述步骤串起来, $P_d$ 用 $P_c$ 表示出来,即有
\[\begin{equation}\begin{split} \begin{pmatrix} \boldsymbol{p} \\ 1 \end{pmatrix} &= K P_d = K \distort(P_n) \\ &= K \distort(\frac{1}{Z_c} P_c) \end{split} \tag{3. 畸变模型公式} \end{equation}\]则畸变模型相比针孔相机模型,只需要多求解一个 $\distort$ 函数即可。
2.3 双目相机模型
vslam 中其实是基于图片上的像素坐标,反过来去定位物体在世界坐标系里的位置。然而,畸变模型中将$Z$归一到1的步骤丢掉了物体的深度信息, 计算机无法基于一张平面照片去还原出一个(精确的) 3D 世界。
为什么人似乎可以基于照片推测物体的远近呢?比如知道“手心里的太阳”实际离我们很远很远?因为我们有常识(即先验)。 但常识只能告诉我们谁近谁远(相对值),不能给我们精确的距离。 而且,常识会带来欺骗——比如,通过把房子缩小,奥特曼就被认为是巨人,其实他只是穿上奥特曼衣服的人。因为看起来比房子大太多,常识就在我们的脑子里描绘了巨人的模样。
参考人眼,双目相机模型用两个单目相机分别成像,再利用视差原理来还原物体的深度,如下图所示:
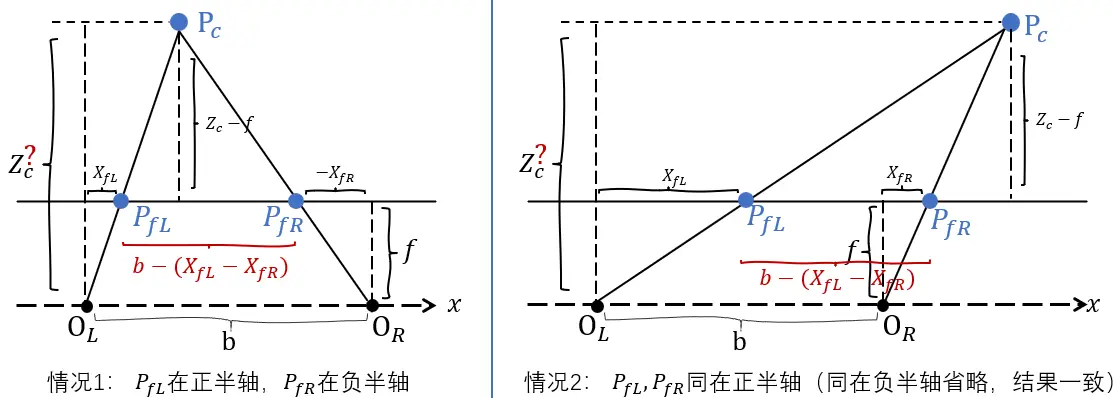
图3: 双目相机模型求解物体深度
两个相机均水平放置,光心相距 $b$, 称其为基线;已知点 $P_c$ 落在两个相机对称成像平面$Z=f$上的点分别为 $P_{fL} = (X_{fL}, Y_{fL}, f)$, $P_{fR} = (X_{fR}, Y_{fR}, f)$,求解 $Z_c$ 的值。
根据 $\triangle P_cP{fL}P_{fR}$ 和 $\triangle P_cO_LO_R$ 相似,有
\[\begin{align*} \frac{Z_c - f}{Z_c} &= \frac{\overline{P_{fL}P_{fR}}}{\overline{O_LO_R}} \\ & \scriptstyle{\text{//上图可知, 不论何种情况,}\;\overline{P_{fL}P_{fR}}\; =\; b - (X_{fL}-X_{fR})} \\ &= \frac{b - (X_{fL} - X_{fR})}{b} \end{align*}\]求解 $Z_c$, 得
\[\newcommand{\eqdef}{\operatorname{\overset{def}{=}}} Z_c = \frac{f b}{d}, \qquad \text{其中}\; d \eqdef X_{fL} - X_{fR} \tag{4. 双目相机模型三角测距}\]上述方法也叫三角测距。 $d = X_{fL} - X_{fR}$ 被称为视差!由公式看到,视差越大,物体深度越小,反之亦然。这与常识一致。
有几个点需要注意:
-
书上的坐标体系,不确定是像素坐标系还是相机坐标系;理论上深度应该在相机坐标系上计算,但书里又提到
视差最小为1像素。 上面我们是在相机坐标系下描述的。当然二者差别也没那么大——在去畸变后,二者就差一个内参的线性变换。 -
图片最小分辨率是1像素,则视差 $d$ 有最小值;故双目模型可测量的最大距离 $Z_c$ 有极限。
-
双目模型计算深度的难点不在上面公式,而在于如何从两个相机的成像中,匹配到与 $P_c$ 分别对应的 $P_{fL}$, $P_{fR}$. 这也是 vslam 的核心问题。
因为要从两个相机成像中找共同点,因此双目相机模型对物体表面的纹理情况、环境光线强度有较大的依赖,同时匹配时耗时也较大。 下面讲到的 RGB-D 相机直接从硬件层面解决深度值获取的问题。
2.4 RGB-D 相机
这块书上就没整公式了233. 目前 RGB-D 主要有两种实现方式:
| 方式 | 原理 | 代表产品 |
|---|---|---|
| 结构光 Structured Light | 本质就是双目相机的三角测距,只是其会主动发射编码过的光,用于优化双目相机模型对物体表面纹理、环境光线的依赖. | 微软 Kinect 1代,谷歌 Project Tango 1代,Intel RealSense, Apple IPhone X(2017) |
| 飞行时间 ToF, Time-of-Flight | 光速xToF测距 | 微软 Kinect 2代, Apple IPad Pro(2020) |
从 《飞行时间(ToF)传感器技术及应用-2020版》 看,ToF 已经成为主流。
2.5 附录
a. 针孔相机
搜索“针孔相机”,一种是“不正经”的偷拍相机,本质仍然是基于镜头的(可以看看,注意防范);另一种才是针孔相机模型对应的相机。 看维基百科-针孔相机可以具体了解。
从知乎问题-为什么相机普遍没有采用小孔成像原理?它的缺陷在哪儿?里的回答里, 可以看到 Coded Aperture Imaging 这篇有意思的文章(主要是文章比较老了,有那个年代的感觉……)。
b. 畸变原理
在 一种大视场镜头的畸变校正方法 第 1 节,介绍了畸变原理:
畸变是由于镜头的存在而引入的失常…径向畸变产生的主要原因是光学镜头本身径向曲率的变化,从而造成图像的扭曲和形变。
c. CCD/CMOS 及图像数字化
CCD/CMOS 本意是两种半导体技术的称呼,在图像领域也被直接用来指代图像传感器, 在旧文(2016年) 硬货|图像传感器大PK:CCD和CMOS谁更强 中介绍了这两种技术的原理和对比,在现在(2022年),相机基本都使用 CMOS. 无论哪种技术,本质都是完成光到电的转换,在 CMOS图像传感器理解 前部分描述了光电转换基础原理。
在 图像的采样和量化 中图示了图像数字化过程中采样和量化究竟是啥。
d. 为什么转换到像素坐标系时,X轴、Y轴缩放比例一般不同?
网上没有找到确切的答案。总结+猜测有一下几个可能:
- 像素,本来就不是方形 3
- 像素在横、纵的排列间距不同
- 考虑生产过程整体最优解(如制作机器要求像素个数最好是某个数的倍数?)
- 受生产工艺的影响,像素无法小到横纵个数比例刚好和物理比例一致 (基本不可能。从下面的例子可以看到,实际像素个数并非尝试去无限拟合物理比例)
- 生产误差(基本不可能。这大概会引起畸变,但不会引起缩放不一致问题)
在相机标定原理介绍(一)中,有一个通过传感器参数计算横纵缩放的例子: NiKon D700相机,传感器尺寸:36.0×23.9 mm,最大分辨率为4256×2832; 则横向缩放比例 $\alpha = \frac{36.0}{4256} = 8.46e^{-3}$,纵向缩放比例 $\beta = \frac{23.9}{2832} = 8.44e^{-3}$. 这说明,在设计层面,横纵的缩放比例就不同。(PS: 传感器尺寸,就对应到物理长、宽。这个是我没想到的)
e. 其他的分辨率
直观地,我们知道数码相机有分辨率的限制(因为传感器的像素限制),但意外的是,镜头、胶片也有分辨率的限制。
首先是镜头“分辨率”,知乎-OMNI的描述看起来比较可信,内容大致如下: 镜头的分辨率主要体现在镜头解析力上,相机不可能做到无线解析能力。一是因为复杂的光学透镜组存在各种畸变(球差、慧差等等), 二是当光线的波长和障碍物的尺寸相当的情况下,会发生物理学上所说的衍射现象,因此只要是镜头解析力总是有限的。 为了衡量各个镜头的差异当然就需要有些标准来度量镜头的解析能力,当然这个标准可以从很多方面来看,比如常用的线对(lp/mm), 当然可以从频谱上来看,就是调制传输函数(MTF),还可以从物理光学上的瑞利判据进行解释。
然后是胶片“分辨率”,摘取知乎-亦明的回答: 胶片的成像最小单位是银盐晶体颗粒,尺度大约几个到几十个微米,微观上并不是无限细分的。银盐晶体在成像时还会形成团簇排列的二级结构, 进一步降低了有效分辨率。实践中胶片成像之后还要经过显影-定影操作,和印放过程,有效分辨率和信噪比还要进一步打折。 经验估计,普通135胶片的有效分辨率大约相当于300-500万像素的数码照片;用最细颗粒的低感胶片,顶级的镜头,最精密的暗房流程, 能得到相当于1000万像素,甚至接近2000万像素的水平。而现代主流135全画幅数码相机的像素数已经超越了这个水平。
3. 图像
这块就比较偏通用知识了。
图像逻辑上可以看做是矩阵,图宽是矩阵的列(即 $x/u$ 轴),图高是矩阵的行(即 $y/v$ 轴),所以用矩阵规则访问图片时, 先 $y$ 后 $x$ (先 $v$ 后 $u$).
在每个位置上,根据图片类型用不同数据类型表示:
-
灰度图每个位置用 unsigned char (0-255)
-
深度图用 unsigned short(0 - 65535, 对应单位mm,故最大支持65.5m的深度)
-
RGB/BGR/BGRA 图,就是一个元组.
在实现上,图片一般都是连续存储的(类似C的多维数组, 底层其实是一维数组)。
4. OpenCV 在图像上的基础操作
这块就是代码实战了,没啥可说的。
-
见 Pinhole camera geometry,是像素平面上的点。 需要区别于Principal planes and points中透镜上的 principal point. ↩
-
见 wikipedia-distortion. 原始论文,一个是1966年,一个是1919年,年代久远得让人难以置信…… 论文下下来扫了一遍,没找到书上的公式。 大概现在使用的公式是后人不断改进的结果吧。去畸变是一个大的Topic,Brown-Conrady model 应该是最基础的吧。 ↩
-
工业相机标定相关知识整理: 一般情况下相机成像单元不是严格的矩形的,其在水平和垂直方向上的大小是不一致的, 这就导致在X和Y方向上的缩放因子不一样,所以需要分别定义两个缩放因子。对针孔摄像机来讲,表示图像传感器上水平和垂直方向上相邻像素之间的距离。 ↩
