本讲开始,进入到实践应用部分。这节讲基于特征法的视觉里程计。
1 术语表
| 中文名称 | 英文名称 |
|---|---|
| 视觉里程计 | Visual Odometry, VO |
| 关键点 | Key Point, kp |
| 描述子 | Descriptor |
| 角点 | corner |
| 矩 | moment, Image Moment (图像矩) |
| 灰度(值) | intensity |
| 对极几何 | epipolar geometry |
| 极平面, 极点, 极线 | epipolar plane, epipoles, epipolar line |
| 本质矩阵、本征矩阵 | Essential matrix, $\boldsymbol{\mathrm{E}}$ |
2 视觉里程计概述
视觉里程计,根据相邻图像的信息估计出粗略的相机运动。如果有后端,可给后端提供较好的初始值。
算法可分为两大类:特征点法和直接法; 特征点法先抽特征,具有稳定,对光照、动态物体不敏感的优势,但耗时大; 直接法则直接基于像素,少了特征提取步骤,耗时有所改善。
基于特征点法的视觉里程计,分 2 个步骤:
- 提取特征,找到匹配的点
- 基于匹配的点,计算相机的运动(里程计)
3 步骤一:提特征 & 匹配
3.1 概述
首先看什么是特征点?特征点就是图里比较“特别”、关键的点(像素), 一般要具备如下性质:
- 可重复性 (Repeatability): 相同的特征,在两张图中都能找到。没有可重复性,源头上就没法做匹配。
- 可区别性 (Distinctiveness): 不同特征有不同表达。 这个很显然,不可区分,则无法找到唯一匹配。
- 高效率 (Efficiency): 同一张图,特征点数量要远少于像素量。 (难道不是指提特征速度快吗?233)
- 本地性 (Locality): 特征仅与一小片区域有关。(就是局部特征吧,难道不可以提全局特征吗?233)
如何匹配?先要把提出的特征,用可度量的形式表示出来,然后用相应的度量函数计算特征间相似度/距离,最相似/距离最近的,就是匹配的特征点。 一般来说,特征都被表示为数值型向量;如果数值类型取浮点数,那么通常就用余弦相似度来做度量;而如果是 0/1 向量,就用汉明距离。
整个提特征的实际流程概述如下:
- 从图里提特征,每个特征计算2个关键信息:关键点、描述子。关键点是特征点在图像中的位置,还可能包括朝向、大小信息;描述子是特征表示,即向量。
- 对两张图里提出的所有特征,逐个基于描述子找匹配的特征,经过一定过滤后,得到一个关键点对集合 $\{(kp_{1i}, kp_{2i}) \vert i=0,1,\cdots \}$.
下面具体展开。
3.2 ORB 方法提特征
书上列了几个特征提取方法,如:
- FAST (Features from Accelerated Segment Test), 只能检测角点, 特征不稳定
- SIFT (Scale-Invariant Feature Transform), 效果好,但速度慢,在SLAM里目前还不实用
-
ORB (Oriented FAST and Rotated BRIEF), 质量和性能的折衷,在 SLAM 中比较有优势
大名鼎鼎的 ORB-SLAM 就基于此,且以此命名。在 ORB-SLAM 论文中写到: Use of the same features for all tasks: tracking, mapping, relocalization and loop closing. This makes our system more efficient, simple and reliable. We use ORB features which allow real-time performance without GPUs, providing good invariance to changes in viewpoint and illumination.
书里主要介绍的也是 ORB 方法。ORB 最早来自 ICCV 2011 的论文 ORB: an efficient alternative to SIFT or SURF, 如名字,它将 FAST 和 BRIEF 方法结合起来,并分别做了改进。
首先是对 FAST 的改进: Oriented FAST. 原始 FAST 是在像素粒度,检测周围是否有一定数量的连续像素与中心像素有一致性的亮度差异; 如果有,就将其当做角点的候选。接着,轮询每一个候选角点,如果此点的差异比周围点(半径为1的范围)都更明显, 就判定此点为角点(这个步骤称为nonmax-suppression, 非极大值抑制)。
完整的 FAST 算法,可以参见 Fast OpenCV Tutorial. OpenCV 实现的 FAST, 并没有完全遵循原论文, 其抛弃了论文中用 ID3 决策树确定最佳筛选顺序的逻辑,直接按规则写死了筛选顺序(FAST 原论文叫 Machine learning for high-speed corner detection, 这下直接把 ML 部分给去了 :dog:). OpenCV FAST 源码解析,有兴趣可看OpenCV FAST 角点检测算法 CPU 版本实现源码注解
FAST 简单高效,但有缺陷,书上说是“分布不均匀,重复性不强”。 ORB 里针对 FAST 的缺陷主要做了如下两点改进:
| 角点无方向,导致描述子不具备旋转不变性 | 通过灰度质心法 (Intensity Centroid) 计算方向, Oriented FAST 名称的由来 |
| 取固定半径,导致特征无尺度不变性:远看像角点,近看就不是角点了 | 构建图像金字塔 |
灰度质心法,就是以特征点为中心 $O$,取围着的一块矩形(一般正方形)区域。计算矩形区域内灰度质心点 $C$, 则 $\overrightarrow{OC}$ 便是此特征点的方向。有此方向,就可以实现旋转不变性。灰度质心法也被简写为IC. 书上基于图像矩来计算灰度质心:
\[\begin{align} M_{pq} &= \sum_{x} \sum_{y} x^{p}y^{q} \mathop{I}(x, y) \\ C &= \left (\frac{M_{10}}{M_{00}}, \frac{M_{01}}{M_{00}} \right ) \end{align} \tag{1. 基于图像矩求解灰度质心}\]其中 $x, y$ 是图像中各个像素的坐标(这时一般将图像中心作为坐标原点),$\mathop{I}(x, y)$ 是此坐标处的像素灰度值。
这里我们稍微展开下。我看到书上这段描述的时候,有两个疑惑点,其一是为什么用灰度质心法就可以实现旋转不变性,其二是图像矩是什么?为何可以据此计算灰度质心呢?下面记录下自己的学习、不可靠猜想的过程。
首先是为何 IC 可以实现旋转不变性。这其实可以进一步展开成 2 个问题:1. 为什么计算旋转角度可得到旋转不变性? 2. 为什么可以用灰度质心法计算角度?
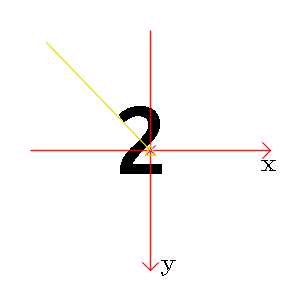
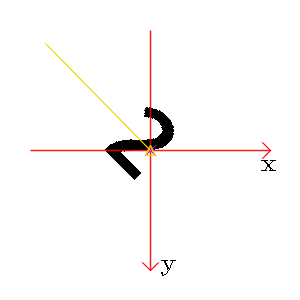
图1: 正立的“2”和顺时针旋转45度的“2”
从“2”的一横我们很容易看到旋转的角度;但是,如果我们用灰度质心法计算角度,却发现二者基本没有差别(前者-133.97 度,后者 -134.61 度)。这似乎说明灰度质心法计算旋转角度是有一定局限性的。
我们以一个写着“2”的图片举例。第一个时刻(第一张图)2是正的(旋转0度),第二个时刻2是斜着的(旋转了45度),我们怎么让两个时刻的“2”匹配上呢(也就是旋转不变)?显然,我们可以先算出每个时刻2的旋转角度,然后在匹配前都先把2反向旋转回去,这样得到两个时刻都是正的“2”,就好匹配了!这回答了为什么计算旋转角度可得旋转不变。这里的“旋转角度”,用更标准地说法,应该是 orientation (方向). 接着再看为何可以用 IC 算 orientation. 我们可以把一块图片看做一个方形饼干,图像上的每个像素就是构成饼干的小粒,而像素强度就是饼干粒的质量。这个图像五彩斑斓/黑白分明,对应着饼干里面不同位置有不同的材质(有的地方只有面粉,有的还有夹心、葡萄干)。因为饼干质量分布不均匀,所以它的质心不在中心点(当我们想要把饼干平稳放在指尖时,就不能去选中心位置),且只要我们不吃它,饼干质心点相对中心的方向不因为我们旋转饼干而发生变化。也即,中心到质心的连线,随整体旋转而旋转。回到图片,也就是说用灰度质心法找到 $\overrightarrow{OC}$, 就能表示整个图片的 orientation 了。其实去 ORB 原始论文看,IC 引自Measuring corner properties, 在此文中,计算 corner 的 orientation 有两种方法:灰度质心法、梯度质心法。ORB 选择了简单又高效的灰度质心法,甚至把原文基于背景色做角度调整的操作也去了。
再看为何基于图像矩可以算灰度质心?我看了下 wikipedia 的 image moment, 感觉这是一个需要记忆的概念,不好理解。 不过既然是“质心”,那肯定也可以从普通物体计算质心的公式来推导上面的结果吧。 根据 Center of mass 中 definition 部分,物体质心坐标为
\[C = \frac{1}{M}\sum_{i=1}^{n} m_i r_i\]其中,$n$ 是质点个数,$m_i$ 是质点$i$的质量, $r_i$ 是相应坐标,$M = \sum_{i=1}^{n} m_i$ 表示所有质点质量(值的)和。 如前面所说,我们认为每个像素就是质点,其灰度值就是质量,坐标用$(x, y)$ 二维直角坐标系表示,则带入此质心坐标计算公式,就得到了前面的基于图像矩计算的公式。所以,如果理解不了图像矩,也可以从质心公式(这个更直观?)出发来看这个结果。
最后,我自己也试验了下灰度质心法算旋转角度。如图2,很不凑巧,灰度质心法在“2”的例子上效果不好。简单思考下,灰度质心法显然是有局限性的:
-
它必须要求图片灰度分布不均匀、质心偏离中心才行,这样中心与质心的连线才会随旋转而改变。极端情况下,假设图片就是一块纯白色,那不管我们旋转多少度,灰度质心法算出的两张图片旋转角度的差一定是0,因为全白图片质心和中心重叠,无法计算角度。我又试了下左边黑、右边白的大色块,灰度质心法算出的旋转角度就非常精准。
-
图片块像素的量的分布随旋转不能发生变化。这个在实际中影响较大——因为图片是方的,一旦让图片绕某个点旋转,则部分像素可能会从图片框里移除,新的像素(其他块)会补上来。这导致旋转前后像素都不同了,质心计算肯定就不准了。
当然,我的测试也很有问题——图片太大、整体灰度差异不显著。因为 ORB 的处理对象是 corner(小,且灰度变化显著), 而且 SLAM 时两张图片间差异也较小,所以上述两个问题应该影响没那么大。
用图像字塔法(Pyramid)来优化无尺度不变性的问题. 这是一种比较通用的方法,所谓“金字塔”,即对原始图片进行不同级别地缩放,然后在不同缩放级别的结果上做 FAST 匹配,各层叠加起来就像一个金字塔。用上面的图片实际测试了下,金字塔法真的非常重要!
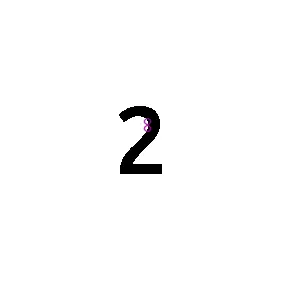
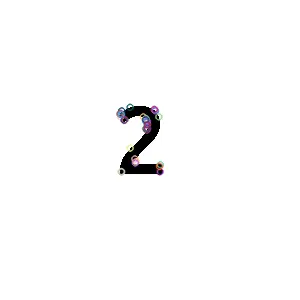
图2: 无金字塔(左)和 4 层金字塔(右)下“数字2”图片的角点匹配效果
可以看到,不使用金字塔,匹配的角点非常少!而 4 层的金字塔,人工认为的角点基本覆盖了。这说明 FAST 角点检测受尺度影响很大。
FAST优化之外, ORB 用优化后的 BRIEF (rBRIEF) 来计算描述子。BRIEF, 即 Binary Robust Independent Elementary Features. 它对图片里的一批点对,用简单的布尔测试,得到一个表示。这些表示对 lighting, blur, and perspective distortion 都能得到比较鲁棒的结果,但对 in-plane rotation 处理不太好。 所以 ORB 这里就增加了前面 Oriented FAST 得到的方向信息,在计算 BRIEF 之前先反向旋转一下, 即得到被称为 Steered BRIEF 的表示。 除此之外,我们还要解决一个问题——如何选这些匹配对呢? BRIEF 在一个 patch 中,在关键点周围选点对的,显然,这样的点对非常多, 需要有一个方法来挑选出这些点对。 ORB 的作者通过实验,确定了如下选点对的标准:
- 这个测试对在测试集的所有图片上测试的结果(是一个0/1序列),方差应尽可能大(从而有区分性),且均值应该靠近0.5
- 这些测试对之间应该尽可能(统计)无关,否则更多的点对就没有意义
围绕这个目标作者设计了一个贪心算法来选择点对,最终得到了 256 尽可能满足上述条件的匹配对, 这些对是2个相对中心点的坐标,构成了 ORB 计算描述子的方法,在论文中被称为 rBRIEF. 最终 rBRIEF 生存描述子的过程如下:
- 取出预先设置好的 256 个点对 $P = {(p_l, p_r), \cdots }, \vert P \vert = 256$
- 对每个点对 $(p_l, p_r)$, 先计算反向旋转后的值 $(p_{lr}, p_{rr})$, 然后取 patch 中这两个位置的灰度值 $I_l$, $I_r$.
比较此灰度值,得到此点对对应的特征值:
feat = I_l < I_r ? 1 : 0 - 最终得到 256 维的布尔向量, 即为此特征点的描述子
在 OpenCV 实现中, ORB compute 之后得到的描述子(列表)是一个 cv::Mat, 是一个 (n-features, 8) 的 8UC1, 即用 8 个 unsinged char 来存储这 256 维的特征。在高博的代码里也是这样做的。
3.3 特征匹配
得到两张图像各自 (关键点,描述子) 的列表后,下面就是要通过特征向量的匹配来找到在两幅图中对应的点。向量匹配,就属于 ANN 的范畴了。 暴力匹配是最精确、直接的结果;近似近邻匹配则是更现实的选择。ANN 现在在DNN领域已经非常普遍,底层库一般常用 faiss, 书里说的 FLANN 也是一个选择吧。
我们对第一张图里的每一个点,在第二个图中找到最相近的点,就得到了最原始的匹配结果。然而,这里面显然存在很多误匹配的情况。除去系统(如ANN)误差,主要应该还是
- 不是每个点都有对应的匹配点(比如点在第二张图里看不见了)
- 特征表示的效果不可能让每个点都能找到正确的匹配(描述子计算的局限性)
- 场景本身区分性小(如图片是重复的纹路)
因此我们需要过滤掉误匹配的对。书里通过一个简单的启发式规则 d <= max(2 * min_dist, 30) 来过滤。我想,如果我们可以假定两张图片的拍摄时间是比较近的时刻/或是双目同时刻,或许可以在像素位置上限定匹配的距离。这个应该有很多方法,可以具体情况具体处理。但无论如何处理,剩余的点对应该还是有噪声的。所以,后续计算相机运动的部分,需要考虑噪声的存在。
如求解2D-2D间运动的对极几何方法,可以用 RANSAC (rando sample consensus) 算法来找到 outlier, 来消除/减弱噪声对估计的影响。同时反过来,这些方法其实也反过来对“匹配是否是噪声”给出了一个预测。

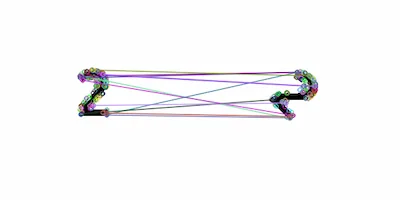
图3: “数字2”的使用ORB的匹配情况
Good Match的距离阈值为 11. 可以看到,误匹配比较严重。应该主要还是特征点太相似了
4 计算相机运动
基于前后时刻两帧的一组特征匹配点,我们可以用来估计相机的运动,即计算 $R$, $t$, $P_w$.
根据点的类型,估计的方法可以分为对极几何, PnP, ICP.
4.1 对极几何 (2D-2D)
给定无深度的来自同一个相机的图片1、图片2和两个图片中的匹配点对 $\left \{(p_{1i}, p_{2i})\; \vert\; i = 1, 2, \cdots \right \}$,求解
- 图片1到图片2的坐标变换 $R$, $t$
- 点深度
如果图片1、图片2是单目前后两帧的图片,则 $R$, $t$ 就是相机的运动。如果图片1、图片2是双目相机的左右图片,则主要得到解物体的深度。
来自同一个相机,即约束相机内参一致;其实也可以来自不同相机,这时需要预处理,保证二者在一个坐标系里。
一种漂亮的求解方法,就是对极几何。其定义了同一个物体 $P_c$ 和两个相机的光心 $O_1$, $O_2$、归一化成像平面上的像 $x_{1i}$, $x_{2i}$ 构成的平面。基于这个空间平面的性质,对上述变量有如下约束:
$\newcommand{\bs}{\boldsymbol}$
\[\rm x_{2i}^T E x_{1i} = 0 \tag{1. 对极约束}\]其中
\[\rm E = \bs{t}^\wedge R \tag{2. 本质矩阵}\]被称为本质矩阵、本征矩阵。$ \bs{t}^\wedge $ 是平移向量 $\bs t$ 的反对称矩阵(3rd有讲)。注意 $x_{1i}$, $x_{2i}$ 分别是图1、图2对应的归一化平面上的点,即 $x_{1i} = K^{-1} p_{1i}$, $p_{1i}$ 是图1上的像素点;同理 $x_{2i}$. 还要注意 $x_{2i}$ 在左边, $x_{1i}$ 在右。
可以这样记:一般这种变换,都是从右往左看的. 因为我们是算图1到图2的变换,故图1的点在右。
又归一化平面上的点 $x_i = K^{-1} p_i$,所以有基础矩阵 $F = K^{-1}EK^{-1}$, $p_{2i}^{T} F p_{1i} = 0$, 其中 $K$ 是相机内参,而 $p_i$ 就是(去畸变后的)像素坐标。实际来看,$F$ 似乎用得也挺多的,因为它直接关联了像素坐标,更直接。
上述公式的推导,建议看 从零开始一起学习SLAM | 不推公式,如何真正理解对极约束?,书感觉并不是那么易懂。
经过多个资料的阅读,对极几何就是表示了空间点$P$和其在两个相机归一化平面上的投影点$x_1$, $x_2$ 在一个平面上的这一“显然”关系。特别的, $Ex_1$ 就是在平面2上点 $x_1$ 对应的极线 $l_2$; 而 $x_{2}^T E x_1 = x_{2}^T l_2 = 0$ 就是表示 $x_{2}$ 在极线 $l_2$ 上(点到直线距离为0)。 所有的极线,都会交于极点,因为极点就是两个光心连线与各自成像平面的角点,肯定是唯一的。极点不一定在图像上,可以在图像外。
参看 opencv::computeCorrespondEpilines api,可知 $E x_1$ 就是极线。不过 Opencv 这里用的是基础矩阵 $F$, 这样它计算出的极线,就不是在归一化平面上,而是直接就在像素平面上了。在 Tutorial: Epipolar Geometry In simple words, Fundamental Matrix F, maps a point in one image to a line (epiline) in the other image. 也验证了此点。
